活动一:忆一忆,说一说
1. 请你列举生活中常见的三角形形状的物体.
2. 你是如何定义三角形的?
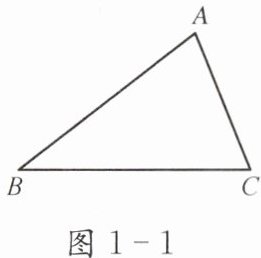
3. 如图1-1,三角形可以表示为
1. 请你列举生活中常见的三角形形状的物体.
屋顶、三脚架、自行车车架等(合理即可)
2. 你是如何定义三角形的?
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形
3. 如图1-1,三角形可以表示为
△ABC
,三条边分别为AB、BC、AC
,三个内角分别为∠A、∠B、∠C
,AB 的对角为∠C
,∠B 的对边为AC
.
答案:1. 屋顶、三脚架、自行车车架等(合理即可);2. 由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形;3. △ABC;AB、BC、AC;∠A、∠B、∠C;∠C;AC
解析:
1. 生活中常见的三角形形状物体有屋顶、三脚架、自行车车架等(列举合理即可)。
2. 由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
3. 图中三角形可表示为△ABC;三条边分别为AB、BC、AC;三个内角分别为∠A、∠B、∠C;AB的对角为∠C;∠B的对边为AC。
2. 由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
3. 图中三角形可表示为△ABC;三条边分别为AB、BC、AC;三个内角分别为∠A、∠B、∠C;AB的对角为∠C;∠B的对边为AC。
活动二:画一画,议一议
1. 阅读课本第4页的"尝试",回答下列问题.
(1)是不是任意三条线段都能组成一个三角形?
(2)三条线段满足什么条件才能组成一个三角形?
由此得出三角形的三条边之间的关系:
2. 三角形的任意两边之差与第三边有什么关系?你能证明吗?
1. 阅读课本第4页的"尝试",回答下列问题.
(1)是不是任意三条线段都能组成一个三角形?
不是
(2)三条线段满足什么条件才能组成一个三角形?
任意两条线段之和大于第三条线段
由此得出三角形的三条边之间的关系:
三角形任意两边之和大于第三边
.本结论的理论依据是:两点之间,线段最短
.2. 三角形的任意两边之差与第三边有什么关系?你能证明吗?
三角形任意两边之差小于第三边;证明过程见解析。
答案:1.(1)不是;(2)任意两条线段之和大于第三条线段;三角形任意两边之和大于第三边;两点之间,线段最短。2.三角形任意两边之差小于第三边;证明过程见解析。
解析:
1.(1)不是任意三条线段都能组成一个三角形。
(2)三条线段中任意两条线段之和大于第三条线段才能组成一个三角形。三角形的三条边之间的关系:三角形任意两边之和大于第三边。本结论的理论依据是:两点之间,线段最短。
2.三角形任意两边之差小于第三边。证明:设三角形的三条边分别为$a$、$b$、$c$,由三角形任意两边之和大于第三边可得$a + b > c$,移项得$c < a + b$;$a + c > b$,移项得$b < a + c$;$b + c > a$,移项得$a < b + c$。将上述三个不等式变形可得$c - a < b$,$b - a < c$,$a - b < c$等,即三角形任意两边之差小于第三边。
(2)三条线段中任意两条线段之和大于第三条线段才能组成一个三角形。三角形的三条边之间的关系:三角形任意两边之和大于第三边。本结论的理论依据是:两点之间,线段最短。
2.三角形任意两边之差小于第三边。证明:设三角形的三条边分别为$a$、$b$、$c$,由三角形任意两边之和大于第三边可得$a + b > c$,移项得$c < a + b$;$a + c > b$,移项得$b < a + c$;$b + c > a$,移项得$a < b + c$。将上述三个不等式变形可得$c - a < b$,$b - a < c$,$a - b < c$等,即三角形任意两边之差小于第三边。
活动三:做一做,想一想
1. 如图1-2,在△ABC中,AB>AC,通过动手操作比较∠B和∠C的大小.

2. 通过刚才的探究,你发现了怎样的结论?
1. 如图1-2,在△ABC中,AB>AC,通过动手操作比较∠B和∠C的大小.

2. 通过刚才的探究,你发现了怎样的结论?
答案:∠C>∠B;在三角形中,较长的边所对的角较大。
解析:
1. 动手操作:将△ABC 沿过点 A 的直线折叠,使 AC 落在 AB 上,点 C 的对应点落在 AB 上,此时可观察到∠C 的一部分与∠B 重叠,且∠C 未重叠部分大于 0,故∠C>∠B;2. 结论:在三角形中,较长的边所对的角较大。