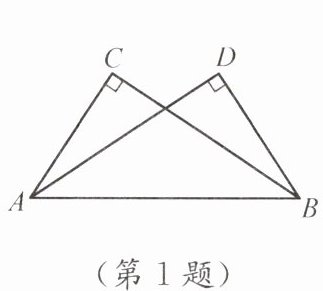
1. 如图,∠ACB= ∠ADB= 90°,要使△ABC≌△BAD,还需增加一个什么条件?把增加的条件填在横线上,并在括号内填上判定全等的理由.
(1)
(3)
(1)
AC=BD
(HL
);(2)BC=AD
(HL
);(3)
∠CAB=∠DBA
(AAS
);(4)∠CBA=∠DAB
(AAS
).
答案:(1)AC=BD (HL);
(2)BC=AD (HL);
(3)∠CAB=∠DBA (AAS);
(4)∠CBA=∠DAB (AAS)。
(2)BC=AD (HL);
(3)∠CAB=∠DBA (AAS);
(4)∠CBA=∠DAB (AAS)。
2. 如图,点A,B,C在一条直线上,∠A= ∠C= 90°,AB= CD,再增加一个条件

AE=CB(答案不唯一)
,可得△EAB≌△BCD.
答案:可添加的条件为:AE=CB(答案不唯一)。
证明:
在$\triangle EAB$和$\triangle BCD$中,
$\begin{cases}AE = CB,\\\angle A=\angle C = 90^{\circ},\\AB = CD.\end{cases}$
根据$SAS$(边角边)全等判定定理,可得$\triangle EAB\cong\triangle BCD$。
故答案为:$AE = CB$(答案不唯一)。
证明:
在$\triangle EAB$和$\triangle BCD$中,
$\begin{cases}AE = CB,\\\angle A=\angle C = 90^{\circ},\\AB = CD.\end{cases}$
根据$SAS$(边角边)全等判定定理,可得$\triangle EAB\cong\triangle BCD$。
故答案为:$AE = CB$(答案不唯一)。
3. 如图,在△ABC和△BCD中,∠ACB= ∠DBC= 90°,E是BC的中点,ED⊥AB,垂足为F,且AB= DE.
(1) 求证:BD= CB.
(2) 若BD= 8,求AC的长.

(1) 求证:BD= CB.
(2) 若BD= 8,求AC的长.

答案:(1)证明:∵ED⊥AB,∴∠EFB=90°,∴∠DEB+∠ABC=90°.
∵∠ACB=90°,∴∠A+∠ABC=90°,∴∠A=∠DEB.
在△ACB和△EBD中,
$\left\{\begin{array}{l}∠A=∠DEB\\∠ACB=∠EBD=90°\\AB=DE\end{array}\right.$
∴△ACB≌△EBD(AAS),∴BD=CB.
(2)∵BD=8,由(1)知BD=CB,∴CB=8.
∵E是BC中点,∴BE=$\frac{1}{2}$CB=4.
∵△ACB≌△EBD,∴AC=BE=4.
(2)AC的长为4.
∵∠ACB=90°,∴∠A+∠ABC=90°,∴∠A=∠DEB.
在△ACB和△EBD中,
$\left\{\begin{array}{l}∠A=∠DEB\\∠ACB=∠EBD=90°\\AB=DE\end{array}\right.$
∴△ACB≌△EBD(AAS),∴BD=CB.
(2)∵BD=8,由(1)知BD=CB,∴CB=8.
∵E是BC中点,∴BE=$\frac{1}{2}$CB=4.
∵△ACB≌△EBD,∴AC=BE=4.
(2)AC的长为4.
4. 如图,在Rt△ABC中,∠C= 90°,AD= AC,DE⊥AB,交BC于点E. 若∠B= 28°,则∠AEC= ______°.


59
答案:在Rt△ABC中,∠C=90°,∠B=28°,
∴∠CAB=90°-∠B=62°.
∵DE⊥AB,∴∠ADE=90°.
在Rt△ACE和Rt△ADE中,
AC=AD,AE=AE,
∴Rt△ACE≌Rt△ADE(HL).
∴∠CAE=∠DAE=∠CAB/2=62°/2=31°.
在Rt△ACE中,∠C=90°,∠CAE=31°,
∴∠AEC=90°-∠CAE=90°-31°=59°.
59
∴∠CAB=90°-∠B=62°.
∵DE⊥AB,∴∠ADE=90°.
在Rt△ACE和Rt△ADE中,
AC=AD,AE=AE,
∴Rt△ACE≌Rt△ADE(HL).
∴∠CAE=∠DAE=∠CAB/2=62°/2=31°.
在Rt△ACE中,∠C=90°,∠CAE=31°,
∴∠AEC=90°-∠CAE=90°-31°=59°.
59
5. 已知:如图,点A,D,B,F在一条直线上,AC= FE,AD= FB,∠C= ∠E= 90°.
求证:AC//EF.

求证:AC//EF.

答案:证明:
因为$AD=FB$,所以$AD+DB=FB+DB$,即$AB=FD$。
在$\bigtriangleup ACB$和$\bigtriangleup FDE$中,$\begin{cases}AC=FE\\\angle C=\angle E = 90^{\circ}\\AB=FD\end{cases}$
根据“HL”定理,可得$\bigtriangleup ACB\cong\bigtriangleup FDE$。
所以$\angle A=\angle F$。
因为内错角相等,两直线平行,所以$AC// EF$。
因为$AD=FB$,所以$AD+DB=FB+DB$,即$AB=FD$。
在$\bigtriangleup ACB$和$\bigtriangleup FDE$中,$\begin{cases}AC=FE\\\angle C=\angle E = 90^{\circ}\\AB=FD\end{cases}$
根据“HL”定理,可得$\bigtriangleup ACB\cong\bigtriangleup FDE$。
所以$\angle A=\angle F$。
因为内错角相等,两直线平行,所以$AC// EF$。