活动一:画一画 试一试
记活动一中所画的角为∠AOB,折痕为OC;在∠AOB的内部任意取折痕OC上的一点P,分别画点P到OA和OB的垂线段PD,PE(图1-21),再沿原折痕折叠.
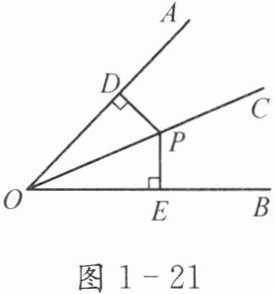
(1)线段PD与PE相等吗?说说你的理由.
(2)由此,你得出什么结论?请用文字表述.
结论:
(3)你认为上述结论成立的条件是什么?请用图1-21中的字母表示.
记活动一中所画的角为∠AOB,折痕为OC;在∠AOB的内部任意取折痕OC上的一点P,分别画点P到OA和OB的垂线段PD,PE(图1-21),再沿原折痕折叠.

(1)线段PD与PE相等吗?说说你的理由.
(2)由此,你得出什么结论?请用文字表述.
结论:
角平分线上的点到角两边的距离相等。
.(3)你认为上述结论成立的条件是什么?请用图1-21中的字母表示.
答案:角平分线上的点到角两边的距离相等。
解析:
(1)由折叠可知,$\angle DOC=\angle EOC$,
因为$\angle AOB=\angle AOC+\angle BOC=2\angle DOC+2\angle EOC$,
所以$\angle AOC=\angle BOC$,
根据角平分线的性质,点$P$在$\angle AOB$的角平分线上,
点$P$到$OA$和$OB$的距离相等,
即$PD=PE$。
(2)角平分线上的点到角两边的距离相等。
(3)点$P$在$\angle AOB$的角平分线上,$PD\perp OA$,$PE\perp OB$。
因为$\angle AOB=\angle AOC+\angle BOC=2\angle DOC+2\angle EOC$,
所以$\angle AOC=\angle BOC$,
根据角平分线的性质,点$P$在$\angle AOB$的角平分线上,
点$P$到$OA$和$OB$的距离相等,
即$PD=PE$。
(2)角平分线上的点到角两边的距离相等。
(3)点$P$在$\angle AOB$的角平分线上,$PD\perp OA$,$PE\perp OB$。
我们知道,如果点P在线段AB的垂直平分线上,那么______;反过来,如果QA= QB,那么点Q在______.
如果点P在∠AOB的平分线上,那么点P到OA,OB的距离相等;反过来,你能提出什么猜想?你的猜想正确吗?尝试说明.
如果点P在∠AOB的平分线上,那么点P到OA,OB的距离相等;反过来,你能提出什么猜想?你的猜想正确吗?尝试说明.
该猜想的正确的。
答案:
该猜想的正确的。
该猜想的正确的。
解析:
首先,我们分析题目给出的信息。
如果点P在线段AB的垂直平分线上,根据垂直平分线的定义,点P到线段AB的两个端点的距离是相等的,即$PA = PB$。
反过来,如果$QA = QB$,那么点Q到线段AB的两个端点的距离相等,根据垂直平分线的性质,我们可以得出点Q必定在线段AB的垂直平分线上。
对于角平分线的情况,题目给出如果点P在$\angle AOB$的平分线上,那么点P到OA,OB的距离相等。
我们可以提出反过来的猜想:如果点P到$\angle AOB$的两边OA, OB的距离相等,那么点P在$\angle AOB$的平分线上。
为了证明这个猜想,我们可以按照以下步骤进行:
第一步,过点P作$PD \perp OA$,$PE \perp OB$,垂足分别为D,E。
第二步,根据题目条件,我们知道$PD = PE$。
第三步,连接OP。由于$PD = PE$,且$\angle ODP = \angle OEP = 90^\circ$,同时OP是公共边,所以根据HL全等条件,我们可以得出$\triangle ODP \cong \triangle OEP$。
第四步,由于$\triangle ODP \cong \triangle OEP$,根据全等三角形的对应角相等,我们可以得出$\angle DOP = \angle EOP$。
第五步,根据角的平分线的定义,若一条射线将一个角分为两个相等的角,则这条射线是这个角的平分线。所以,OP是$\angle AOB$的平分线。
综上,我们证明了如果点P到$\angle AOB$的两边OA, OB的距离相等,那么点P在$\angle AOB$的平分线上。
1. 到三角形的三条边距离相等的点是(
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
A
)A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
答案:A
解析:
根据角平分线的性质,角的平分线上的点到这个角的两边的距离相等。因此,三角形三个角的平分线交于一点,这一点到三角形的三条边距离相等。