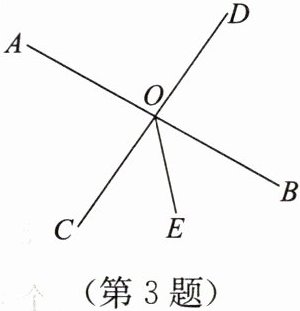
3. 如图,直线AB,CD相交于点O,OE是$\angle BOC$的平分线,且$\angle BOE= 48^{\circ}$,则$\angle AOC= $(
A.$84^{\circ}$
B.$95^{\circ}$
C.$105^{\circ}$
D.$125^{\circ}$
A
).
A.$84^{\circ}$
B.$95^{\circ}$
C.$105^{\circ}$
D.$125^{\circ}$
答案:A
解析:
∵OE是∠BOC的平分线,∠BOE=48°,
∴∠BOC=2∠BOE=2×48°=96°,
∵直线AB,CD相交于点O,
∴∠AOC+∠BOC=180°,
∴∠AOC=180°-∠BOC=180°-96°=84°。
A
4. 如图,两个直角$\angle AOB$,$\angle COD$有相同的顶点O,给出下列结论:①$\angle AOC+\angle BOD= 90^{\circ}$;②$\angle AOC= \angle BOD$;③若OC平分$\angle AOB$,则OB平分$\angle COD$;④$\angle AOD的平分线与\angle COB$的平分线是同一条射线.其中正确的结论有(

A.4个
B.3个
C.2个
D.1个
B
).
A.4个
B.3个
C.2个
D.1个
答案:B
解析:
设∠AOC=α,∠COB=β,∠BOD=γ。
∵∠AOB=∠COD=90°,
∴α+β=90°,β+γ=90°,
∴α=γ,即∠AOC=∠BOD,②正确;
∠AOC+∠BOD=α+γ=2α,不一定等于90°,①错误;
若OC平分∠AOB,则α=β=45°,γ=α=45°,
∴β=γ=45°,OB平分∠COD,③正确;
∠AOD=α+β+γ=90°+γ=90°+α,其平分线分得的角为(90°+α)/2=45°+α/2,
∠COB=β=90°-α,其平分线分得的角为(90°-α)/2=45°-α/2,
从OA起,∠AOC+∠COB平分线的角=α+45°-α/2=45°+α/2,与∠AOD平分线位置相同,④正确。
正确结论为②③④,共3个。
B
∵∠AOB=∠COD=90°,
∴α+β=90°,β+γ=90°,
∴α=γ,即∠AOC=∠BOD,②正确;
∠AOC+∠BOD=α+γ=2α,不一定等于90°,①错误;
若OC平分∠AOB,则α=β=45°,γ=α=45°,
∴β=γ=45°,OB平分∠COD,③正确;
∠AOD=α+β+γ=90°+γ=90°+α,其平分线分得的角为(90°+α)/2=45°+α/2,
∠COB=β=90°-α,其平分线分得的角为(90°-α)/2=45°-α/2,
从OA起,∠AOC+∠COB平分线的角=α+45°-α/2=45°+α/2,与∠AOD平分线位置相同,④正确。
正确结论为②③④,共3个。
B
5. 如图,已知$\angle AOB= 35^{\circ}$,$\angle BOC= 3\angle AOB$,OD平分$\angle AOC$,求$\angle COD$的度数.


答案:70°
解析:
因为$\angle AOB = 35^{\circ}$,$\angle BOC = 3\angle AOB$,所以$\angle BOC=3×35^{\circ}=105^{\circ}$。
$\angle AOC=\angle AOB + \angle BOC=35^{\circ}+105^{\circ}=140^{\circ}$。
因为OD平分$\angle AOC$,所以$\angle COD=\frac{1}{2}\angle AOC=\frac{1}{2}×140^{\circ}=70^{\circ}$。
$70^{\circ}$
$\angle AOC=\angle AOB + \angle BOC=35^{\circ}+105^{\circ}=140^{\circ}$。
因为OD平分$\angle AOC$,所以$\angle COD=\frac{1}{2}\angle AOC=\frac{1}{2}×140^{\circ}=70^{\circ}$。
$70^{\circ}$