17. 将一副三角尺按如图(1)所示的方式拼接在一起,其中边OA,OC与直线EF重合,∠AOB= 45°,∠COD= 60°.
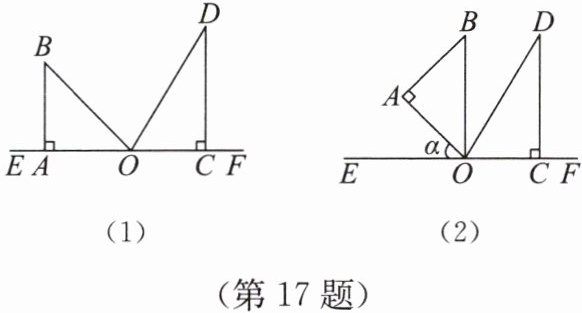
(1)如图(1),∠BOD=
(2)如图(2),三角尺COD固定不动,将三角尺AOB绕着点O按顺时针方向旋转一个角度α,在转动过程中,两个三角尺都在直线EF的上方,当OB平分OA,OC,OD其中的两边组成的角时,求所有满足要求的旋转角度α的值.

(1)如图(1),∠BOD=
75
°;(2)如图(2),三角尺COD固定不动,将三角尺AOB绕着点O按顺时针方向旋转一个角度α,在转动过程中,两个三角尺都在直线EF的上方,当OB平分OA,OC,OD其中的两边组成的角时,求所有满足要求的旋转角度α的值.
旋转角度α的值为30°或90°或105°
答案:(1)
因为$\angle AOB = 45^{\circ}$,$\angle COD = 60^{\circ}$,$\angle AOC=180^{\circ}$。
根据$\angle BOD=\angle AOC-\angle AOB - \angle COD$,则$\angle BOD = 180^{\circ}-45^{\circ}-60^{\circ}=75^{\circ}$。
(2)
情况一:当$OB$平分$\angle AOD$时
旋转后$\angle AOD=(180^{\circ}-\alpha)-60^{\circ}=120^{\circ}-\alpha$,$\angle AOB = 45^{\circ}$。
因为$OB$平分$\angle AOD$,所以$\angle AOB=\frac{1}{2}\angle AOD$,即$45^{\circ}=\frac{1}{2}(120^{\circ}-\alpha)$。
解方程:
首先去括号得$45^{\circ}=60^{\circ}-\frac{1}{2}\alpha$。
然后移项得$\frac{1}{2}\alpha = 60^{\circ}-45^{\circ}$。
即$\frac{1}{2}\alpha = 15^{\circ}$,解得$\alpha = 30^{\circ}$。
情况二:当$OB$平分$\angle AOC$时
旋转后$\angle AOC = 180^{\circ}-\alpha$,因为$OB$平分$\angle AOC$,所以$\angle AOB=\frac{1}{2}\angle AOC$。
已知$\angle AOB = 45^{\circ}$,则$45^{\circ}=\frac{1}{2}(180^{\circ}-\alpha)$。
解方程:
去括号得$45^{\circ}=90^{\circ}-\frac{1}{2}\alpha$。
移项得$\frac{1}{2}\alpha = 90^{\circ}-45^{\circ}$。
即$\frac{1}{2}\alpha = 45^{\circ}$,解得$\alpha = 90^{\circ}$。
情况三:当$OB$平分$\angle DOC$时
已知$\angle DOC = 60^{\circ}$,因为$OB$平分$\angle DOC$,所以$\angle BOC = 30^{\circ}$。
又因为$\angle AOB+\angle BOC+\alpha=180^{\circ}$,$\angle AOB = 45^{\circ}$,则$45^{\circ}+30^{\circ}+\alpha=180^{\circ}$。
解方程:
合并同类项得$75^{\circ}+\alpha=180^{\circ}$。
解得$\alpha = 105^{\circ}$。
综上,(1)$75$;(2)$\alpha$的值为$30^{\circ}$或$90^{\circ}$或$105^{\circ}$。
因为$\angle AOB = 45^{\circ}$,$\angle COD = 60^{\circ}$,$\angle AOC=180^{\circ}$。
根据$\angle BOD=\angle AOC-\angle AOB - \angle COD$,则$\angle BOD = 180^{\circ}-45^{\circ}-60^{\circ}=75^{\circ}$。
(2)
情况一:当$OB$平分$\angle AOD$时
旋转后$\angle AOD=(180^{\circ}-\alpha)-60^{\circ}=120^{\circ}-\alpha$,$\angle AOB = 45^{\circ}$。
因为$OB$平分$\angle AOD$,所以$\angle AOB=\frac{1}{2}\angle AOD$,即$45^{\circ}=\frac{1}{2}(120^{\circ}-\alpha)$。
解方程:
首先去括号得$45^{\circ}=60^{\circ}-\frac{1}{2}\alpha$。
然后移项得$\frac{1}{2}\alpha = 60^{\circ}-45^{\circ}$。
即$\frac{1}{2}\alpha = 15^{\circ}$,解得$\alpha = 30^{\circ}$。
情况二:当$OB$平分$\angle AOC$时
旋转后$\angle AOC = 180^{\circ}-\alpha$,因为$OB$平分$\angle AOC$,所以$\angle AOB=\frac{1}{2}\angle AOC$。
已知$\angle AOB = 45^{\circ}$,则$45^{\circ}=\frac{1}{2}(180^{\circ}-\alpha)$。
解方程:
去括号得$45^{\circ}=90^{\circ}-\frac{1}{2}\alpha$。
移项得$\frac{1}{2}\alpha = 90^{\circ}-45^{\circ}$。
即$\frac{1}{2}\alpha = 45^{\circ}$,解得$\alpha = 90^{\circ}$。
情况三:当$OB$平分$\angle DOC$时
已知$\angle DOC = 60^{\circ}$,因为$OB$平分$\angle DOC$,所以$\angle BOC = 30^{\circ}$。
又因为$\angle AOB+\angle BOC+\alpha=180^{\circ}$,$\angle AOB = 45^{\circ}$,则$45^{\circ}+30^{\circ}+\alpha=180^{\circ}$。
解方程:
合并同类项得$75^{\circ}+\alpha=180^{\circ}$。
解得$\alpha = 105^{\circ}$。
综上,(1)$75$;(2)$\alpha$的值为$30^{\circ}$或$90^{\circ}$或$105^{\circ}$。