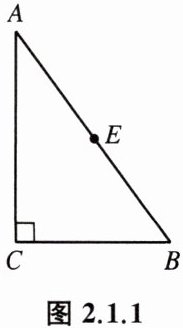
例 如图 2.1.1,在△ABC 中,∠C= 90°,BC= 3 cm,AC= 4 cm,E 为 AB 的中点.
(1) 以点 B 为圆心,BC 长为半径画⊙B,点 A、C、E 与⊙B 有怎样的位置关系?
(2) 以点 A 为圆心,R 为半径画⊙A,若点 B、C、E 中至少有一点在圆内,至少有一点在圆外,则⊙A 的半径 R 应满足什么条件?

(1) 以点 B 为圆心,BC 长为半径画⊙B,点 A、C、E 与⊙B 有怎样的位置关系?
(2) 以点 A 为圆心,R 为半径画⊙A,若点 B、C、E 中至少有一点在圆内,至少有一点在圆外,则⊙A 的半径 R 应满足什么条件?
答案:解:( 1 )
∵$BC=3\ \mathrm {cm},$$AC=4\ \mathrm {cm},$∠C=90°.
∴$AB=5\ \mathrm {cm}$
∵E为AB中点.
∴$BE=\frac {1}{2}AB=\frac {5}{2}\ \mathrm {cm}.$
∴$AC\gt BC,$BE<BC
∴点A在$\odot B$外,点C在$\odot B$上,点E在$\odot B$内.
( 2 )
∵$AB=5\ \mathrm {cm},$$AC=4\ \mathrm {cm},$$AE=\frac {5}{2}\ \mathrm {cm}$
∴$\odot A$的半径R应满足$\frac {5}{2}\ \mathrm {cm}\lt R \lt 5\ \mathrm {cm}$
∵$BC=3\ \mathrm {cm},$$AC=4\ \mathrm {cm},$∠C=90°.
∴$AB=5\ \mathrm {cm}$
∵E为AB中点.
∴$BE=\frac {1}{2}AB=\frac {5}{2}\ \mathrm {cm}.$
∴$AC\gt BC,$BE<BC
∴点A在$\odot B$外,点C在$\odot B$上,点E在$\odot B$内.
( 2 )
∵$AB=5\ \mathrm {cm},$$AC=4\ \mathrm {cm},$$AE=\frac {5}{2}\ \mathrm {cm}$
∴$\odot A$的半径R应满足$\frac {5}{2}\ \mathrm {cm}\lt R \lt 5\ \mathrm {cm}$