6. 已知直径为30 cm的⊙O中有两条平行的弦AB和CD,AB= 18 cm,CD= 24 cm,则弦AB与CD间的距离为
$3\ \mathrm {cm}$或$21\ \mathrm {cm}$
.答案:$3\ \mathrm {cm}$或$21\ \mathrm {cm}$
解析:
情况一:AB、CD在圆心O同侧
过O作OE⊥AB于E,OF⊥CD于F,连接OA、OC。
OA=OC=15 cm,AE=9 cm,CF=12 cm。
OE=$\sqrt{OA^2-AE^2}=\sqrt{15^2-9^2}=12$ cm,
OF=$\sqrt{OC^2-CF^2}=\sqrt{15^2-12^2}=9$ cm,
距离:OE-OF=12-9=3 cm。
情况二:AB、CD在圆心O两侧
距离:OE+OF=12+9=21 cm。
3 cm 或 21 cm
过O作OE⊥AB于E,OF⊥CD于F,连接OA、OC。
OA=OC=15 cm,AE=9 cm,CF=12 cm。
OE=$\sqrt{OA^2-AE^2}=\sqrt{15^2-9^2}=12$ cm,
OF=$\sqrt{OC^2-CF^2}=\sqrt{15^2-12^2}=9$ cm,
距离:OE-OF=12-9=3 cm。
情况二:AB、CD在圆心O两侧
距离:OE+OF=12+9=21 cm。
3 cm 或 21 cm
7. 如图,P是⊙O内的一个定点.
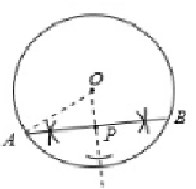
(1)过点P作弦AB,使P是AB的中点(不写作法,保留作图痕迹);
(2)在(1)的条件下,若⊙O的半径为13,OP= 5,求AB的长.
(1)过点P作弦AB,使P是AB的中点(不写作法,保留作图痕迹);
(2)在(1)的条件下,若⊙O的半径为13,OP= 5,求AB的长.

答案:
解:(1)如图所示
(2)连接OA ,如图所示:
因为OP⊥AB .
所以$AP=BP=\sqrt{OA²-OP²}=\sqrt{13²-5²}=12,$
所以AB= 2AP=24
解:(1)如图所示
(2)连接OA ,如图所示:
因为OP⊥AB .
所以$AP=BP=\sqrt{OA²-OP²}=\sqrt{13²-5²}=12,$
所以AB= 2AP=24

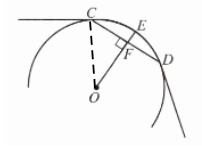
8. 如图,一条公路的转弯处是一段圆弧(即图中$\overset{\frown}{CD}$,点O是$\overset{\frown}{CD}$的圆心),其中CD= 600 m,E是$\overset{\frown}{CD}$上一点,且OE⊥CD,垂足为F,EF= 90 m.求这段弯路的半径.


答案:
解:连接OC,
∵OE⊥CD且$CD=600\,\,\text{m}$
∴$CF=\frac{1}{2}CD=300\,\,\text{m}$
设$OC=OE=\,\,x\,\,\text{m},$则$OF=OE-EF=\left( x-90 \right) \,\,\text{m}$
在Rt△OCF中,
$ OC^2=OF^2+CF^2$
∴$x^2=\left( x-90 \right) ^2+300^2$
解得,x=545
∴$OC=OE=545\,\,\text{m}$
答:这段弯路的半径为$545\,\,\text{m}.$
解:连接OC,
∵OE⊥CD且$CD=600\,\,\text{m}$
∴$CF=\frac{1}{2}CD=300\,\,\text{m}$
设$OC=OE=\,\,x\,\,\text{m},$则$OF=OE-EF=\left( x-90 \right) \,\,\text{m}$
在Rt△OCF中,
$ OC^2=OF^2+CF^2$
∴$x^2=\left( x-90 \right) ^2+300^2$
解得,x=545
∴$OC=OE=545\,\,\text{m}$
答:这段弯路的半径为$545\,\,\text{m}.$

解析:
设这段弯路的半径为$ R $米,则$ OC = OE = R $米。
因为$ OE \perp CD $,$ CD = 600 $米,所以$ CF = \frac{1}{2}CD = 300 $米,$ OF = OE - EF = (R - 90) $米。
在$ Rt\triangle OCF $中,由勾股定理得:$ OC^2 = CF^2 + OF^2 $,即$ R^2 = 300^2 + (R - 90)^2 $。
展开得:$ R^2 = 90000 + R^2 - 180R + 8100 $。
移项化简得:$ 180R = 98100 $,解得$ R = 545 $。
这段弯路的半径为$ 545 $米。
因为$ OE \perp CD $,$ CD = 600 $米,所以$ CF = \frac{1}{2}CD = 300 $米,$ OF = OE - EF = (R - 90) $米。
在$ Rt\triangle OCF $中,由勾股定理得:$ OC^2 = CF^2 + OF^2 $,即$ R^2 = 300^2 + (R - 90)^2 $。
展开得:$ R^2 = 90000 + R^2 - 180R + 8100 $。
移项化简得:$ 180R = 98100 $,解得$ R = 545 $。
这段弯路的半径为$ 545 $米。
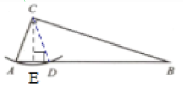
9. 如图,在Rt△ABC中,∠ACB= 90°,AC= 1,BC= $2\sqrt{2}$,以点C为圆心,CA长为半径画弧交斜边AB于点A、D,求BD的长.


答案:
解:作CE⊥AD,垂足为点E,连接CD,
在Rt△ACB中,AC=1,$BC=2\sqrt{2}$
∴$AB=\sqrt{AC^2+BC^2}=3$
∴$CE=\frac {AC×BC}{AB}=\frac {2\sqrt{2}}{3}$
在Rt△CDE中,
∵CD=CA=1,$CE=\frac {2\sqrt{2}}{3}$
∴$DE=\sqrt{CD^2-CE^2}=\frac {1}{3}$
∵CE⊥AD
∴$AD=2DE=\frac {2}{3}$
∴$BD=AB-AD=3-\frac {2}{3}=\frac {7}{3}$
解:作CE⊥AD,垂足为点E,连接CD,
在Rt△ACB中,AC=1,$BC=2\sqrt{2}$
∴$AB=\sqrt{AC^2+BC^2}=3$
∴$CE=\frac {AC×BC}{AB}=\frac {2\sqrt{2}}{3}$
在Rt△CDE中,
∵CD=CA=1,$CE=\frac {2\sqrt{2}}{3}$
∴$DE=\sqrt{CD^2-CE^2}=\frac {1}{3}$
∵CE⊥AD
∴$AD=2DE=\frac {2}{3}$
∴$BD=AB-AD=3-\frac {2}{3}=\frac {7}{3}$

解析:
在Rt△ABC中,∠ACB=90°,AC=1,BC=2√2,由勾股定理得AB=√(AC²+BC²)=√(1²+(2√2)²)=3。
过点C作CE⊥AB于点E,根据三角形面积公式,S△ABC=1/2×AC×BC=1/2×AB×CE,即1/2×1×2√2=1/2×3×CE,解得CE=2√2/3。
在Rt△ACE中,AE=√(AC²-CE²)=√(1²-(2√2/3)²)=1/3。
因为CA=CD=1,CE⊥AD,所以AD=2AE=2/3。
则BD=AB-AD=3-2/3=7/3。
7/3
过点C作CE⊥AB于点E,根据三角形面积公式,S△ABC=1/2×AC×BC=1/2×AB×CE,即1/2×1×2√2=1/2×3×CE,解得CE=2√2/3。
在Rt△ACE中,AE=√(AC²-CE²)=√(1²-(2√2/3)²)=1/3。
因为CA=CD=1,CE⊥AD,所以AD=2AE=2/3。
则BD=AB-AD=3-2/3=7/3。
7/3