9. 如图是由三张大小相同的正方形纸片组成的"品"字形轴对称图案,若正方形纸片的边长是 2 cm,则用一张圆形纸片将该图案完全覆盖时,最小的圆形纸片的半径是
$\frac {5\sqrt{17}}{8}$
.答案:$ \frac {5\sqrt{17}}{8}$
解析:
以图案左下角为原点建立平面直角坐标系,各正方形顶点坐标为:(0,0),(2,0),(2,2),(0,2),(1,2),(3,2),(3,4),(1,4)。设圆心坐标为$(x,y)$,半径为$r$。
由对称性知$x=2$。圆心到点$(0,0)$和$(1,4)$距离相等且为半径,可得方程:
$\sqrt{(2-0)^2+(y-0)^2}=\sqrt{(2-1)^2+(y-4)^2}$
解得$y=\frac{17}{8}$。
半径$r=\sqrt{2^2+\left(\frac{17}{8}\right)^2}=\frac{5\sqrt{17}}{8}$
$\frac{5\sqrt{17}}{8}$ cm
由对称性知$x=2$。圆心到点$(0,0)$和$(1,4)$距离相等且为半径,可得方程:
$\sqrt{(2-0)^2+(y-0)^2}=\sqrt{(2-1)^2+(y-4)^2}$
解得$y=\frac{17}{8}$。
半径$r=\sqrt{2^2+\left(\frac{17}{8}\right)^2}=\frac{5\sqrt{17}}{8}$
$\frac{5\sqrt{17}}{8}$ cm
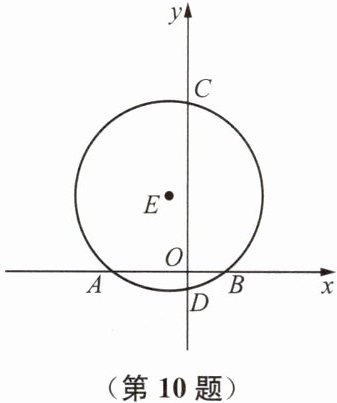
10. 如图,在平面直角坐标系中,直径为 10 的⊙E 交 x 轴于点 A、B,交 y 轴于点 C、D,且点 A、B 的坐标分别为(-4,0)、(2,0).
(1) 求圆心 E 的坐标;
(2) 求点 C、D 的坐标.
(1) 求圆心 E 的坐标;
(2) 求点 C、D 的坐标.

答案:
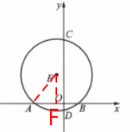
解:(1)作EF⊥AB,垂足为点F,连接AE.
∵A( -4,0 ) ,B( 2,0 )
∴AB=6
∵EF⊥AB
∴$AF=\frac {1}{2}AB=3$
∴点E的横坐标为-4+3=-1
∵$\odot E$的直径为10
∴AE=5
在Rt△AEF 中,∵AE=5,AF=3
∴$EF=\sqrt{AE^2-AF^2}=4$
∴E( -1,4 )
解:( 2 ) 作EG⊥CD,垂足为点G,
连接CE.
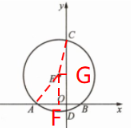
∵E( -1,4 )∴EG=1
在Rt△CEG 中,
∵CE=AE=5,EG=1
∴$CG=\sqrt{CE^2-EG^2}=2\sqrt{6}$
∵EG⊥CD
∴$DG=CG=2\sqrt{6}$
∴C( 0,$4+2\sqrt{6} ) ,$D( 0,$4-2\sqrt{6} ) $
解:(1)作EF⊥AB,垂足为点F,连接AE.
∵A( -4,0 ) ,B( 2,0 )
∴AB=6
∵EF⊥AB
∴$AF=\frac {1}{2}AB=3$
∴点E的横坐标为-4+3=-1
∵$\odot E$的直径为10
∴AE=5
在Rt△AEF 中,∵AE=5,AF=3
∴$EF=\sqrt{AE^2-AF^2}=4$
∴E( -1,4 )

解:( 2 ) 作EG⊥CD,垂足为点G,
连接CE.

∵E( -1,4 )∴EG=1
在Rt△CEG 中,
∵CE=AE=5,EG=1
∴$CG=\sqrt{CE^2-EG^2}=2\sqrt{6}$
∵EG⊥CD
∴$DG=CG=2\sqrt{6}$
∴C( 0,$4+2\sqrt{6} ) ,$D( 0,$4-2\sqrt{6} ) $
解析:
(1)设圆心$E$的坐标为$(x,y)$,因为$A(-4,0)$、$B(2,0)$是$\odot E$与$x$轴的交点,所以$EA=EB$,即$\sqrt{(x + 4)^2 + (y - 0)^2} = \sqrt{(x - 2)^2 + (y - 0)^2}$,两边平方化简得$(x + 4)^2 = (x - 2)^2$,展开得$x^2 + 8x + 16 = x^2 - 4x + 4$,移项合并同类项得$12x = -12$,解得$x = -1$。又因为$\odot E$的直径为$10$,所以半径$r = 5$,$EA = 5$,则$\sqrt{(-1 + 4)^2 + y^2} = 5$,即$\sqrt{9 + y^2} = 5$,两边平方得$9 + y^2 = 25$,解得$y^2 = 16$,$y = \pm 4$。由图可知圆心在$x$轴上方,所以$y = 4$,故圆心$E$的坐标为$(-1,4)$。
(2)设点$C$、$D$的坐标分别为$(0,y_1)$、$(0,y_2)$,因为$C$、$D$在$\odot E$上,所以$EC = ED = 5$。$E(-1,4)$,则$\sqrt{(-1 - 0)^2 + (4 - y_1)^2} = 5$,即$\sqrt{1 + (4 - y_1)^2} = 5$,两边平方得$1 + (4 - y_1)^2 = 25$,$(4 - y_1)^2 = 24$,解得$4 - y_1 = \pm 2\sqrt{6}$,所以$y_1 = 4 + 2\sqrt{6}$,$y_2 = 4 - 2\sqrt{6}$,故点$C$的坐标为$(0,4 + 2\sqrt{6})$,点$D$的坐标为$(0,4 - 2\sqrt{6})$。
(2)设点$C$、$D$的坐标分别为$(0,y_1)$、$(0,y_2)$,因为$C$、$D$在$\odot E$上,所以$EC = ED = 5$。$E(-1,4)$,则$\sqrt{(-1 - 0)^2 + (4 - y_1)^2} = 5$,即$\sqrt{1 + (4 - y_1)^2} = 5$,两边平方得$1 + (4 - y_1)^2 = 25$,$(4 - y_1)^2 = 24$,解得$4 - y_1 = \pm 2\sqrt{6}$,所以$y_1 = 4 + 2\sqrt{6}$,$y_2 = 4 - 2\sqrt{6}$,故点$C$的坐标为$(0,4 + 2\sqrt{6})$,点$D$的坐标为$(0,4 - 2\sqrt{6})$。
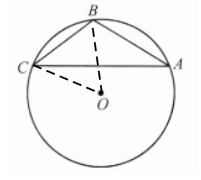
例1 如图2.4.1,△ABC是⊙O的内接三角形,∠A= 30°,BC= 2 cm.求⊙O的半径.


答案:
解:连接OB,OC
∵∠A=30°
∴∠BOC=2∠A=60°
∵OB=OC
∴△OBC是等边三角形
∵$BC=2\,\,\text{cm}$
∴$OB=BC=2\,\,\text{cm},$即$\odot O$的半径为$2\,\,\text{cm}.$
解:连接OB,OC
∵∠A=30°
∴∠BOC=2∠A=60°
∵OB=OC
∴△OBC是等边三角形
∵$BC=2\,\,\text{cm}$
∴$OB=BC=2\,\,\text{cm},$即$\odot O$的半径为$2\,\,\text{cm}.$

解析:
解:连接 $OB$,$OC$。
因为 $\angle A = 30^\circ$,所以 $\angle BOC = 2\angle A = 60^\circ$。
又因为 $OB = OC$,所以 $\triangle OBC$ 是等边三角形。
因此 $OB = BC = 2\,cm$,即 $\odot O$ 的半径为 $2\,cm$。
$2\,cm$
因为 $\angle A = 30^\circ$,所以 $\angle BOC = 2\angle A = 60^\circ$。
又因为 $OB = OC$,所以 $\triangle OBC$ 是等边三角形。
因此 $OB = BC = 2\,cm$,即 $\odot O$ 的半径为 $2\,cm$。
$2\,cm$