1.(1)圆弧的半径为3,弧所对的圆心角为90°,则弧长为
(2)一个扇形的弧长为20πcm,面积为$240πcm^2,$该扇形的半径为
(3)已知扇形的圆心角为120°,它所对的弧长为20πcm,该扇形的半径为
$\frac{3}{2}π$
,扇形的面积为$\frac{9}{4}π$
;(2)一个扇形的弧长为20πcm,面积为$240πcm^2,$该扇形的半径为
24cm
,圆心角为150°
;(3)已知扇形的圆心角为120°,它所对的弧长为20πcm,该扇形的半径为
30
cm,面积为300π
$cm^2.$答案:$\frac{3}{2}π$
$\frac{9}{4}π$
24cm
150°
30
300π
$\frac{9}{4}π$
24cm
150°
30
300π
解析:
(1)$\frac{3}{2}\pi$,$\frac{9}{4}\pi$;
(2)24 cm,$150^\circ$;
(3)30,$300\pi$.
2. 如图,在△ABC中,BC= 4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,且∠EAF= 110°,图中阴影部分的面积是
$4-\frac{11}{9}π$
.答案:$4-\frac{11}{9}π$
解析:
∵⊙A与BC相切于点D,
∴AD⊥BC,AD=2,
∵BC=4,
∴S△ABC=$\frac{1}{2}$×BC×AD=$\frac{1}{2}$×4×2=4,
∵∠EAF=110°,⊙A的半径为2,
∴S扇形EAF=$\frac{110\pi×2^2}{360}$=$\frac{11}{9}\pi$,
∴S阴影=S△ABC-S扇形EAF=4-$\frac{11}{9}\pi$.
4-$\frac{11}{9}\pi$
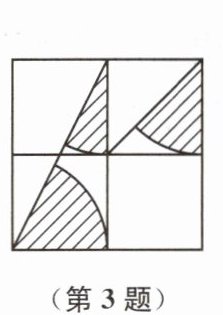
3. 如图,方格纸中4个小正方形的边长均为1,图中阴影部分的面积为
$\frac{3}{8}π$
(结果保留π).
答案:$\frac{3}{8}π$
解析:
由图可知,阴影部分由三个扇形组成。每个小正方形边长为1,左上角扇形半径为1,圆心角为45°;右上角扇形半径为1,圆心角为45°;左下角扇形半径为1,圆心角为45°。
每个扇形面积为$\frac{45}{360}×\pi×1^{2}=\frac{1}{8}\pi$,三个扇形面积之和为$3×\frac{1}{8}\pi=\frac{3}{8}\pi$。
$\frac{3}{8}\pi$
每个扇形面积为$\frac{45}{360}×\pi×1^{2}=\frac{1}{8}\pi$,三个扇形面积之和为$3×\frac{1}{8}\pi=\frac{3}{8}\pi$。
$\frac{3}{8}\pi$
4. 两个圆心角都是90°的扇形OAB和扇形OCD按如图所示的方式叠放在一起,连接AC、BD.若OA= 3,OC= 1,则阴影部分的面积是
2π
.答案:2π
解析:
阴影部分面积为扇形OAB面积减去扇形OCD面积。
扇形OAB面积:$\frac{90^\circ}{360^\circ} × \pi × OA^2 = \frac{1}{4} × \pi × 3^2 = \frac{9}{4}\pi$
扇形OCD面积:$\frac{90^\circ}{360^\circ} × \pi × OC^2 = \frac{1}{4} × \pi × 1^2 = \frac{1}{4}\pi$
阴影部分面积:$\frac{9}{4}\pi - \frac{1}{4}\pi = 2\pi$
2π
扇形OAB面积:$\frac{90^\circ}{360^\circ} × \pi × OA^2 = \frac{1}{4} × \pi × 3^2 = \frac{9}{4}\pi$
扇形OCD面积:$\frac{90^\circ}{360^\circ} × \pi × OC^2 = \frac{1}{4} × \pi × 1^2 = \frac{1}{4}\pi$
阴影部分面积:$\frac{9}{4}\pi - \frac{1}{4}\pi = 2\pi$
2π
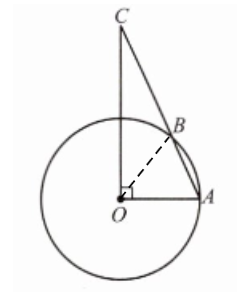
5. 如图,在△AOC中,∠AOC= 90°,∠C= 15°,以点O为圆心,AO为半径的圆交AC于点B,OA= 6.求$\overset{\frown}{AB}$的长.


答案:
解:连接OB,
∵∠AOC=90°,∠C=15°
∴∠A=180°-90°-15°=75°
∵OA=OB
∴∠A=∠OBA=75°
∴∠AOB=180°-75°-75°=30°
∵半径OA=6
∴$\overset{\LARGE{ \frown}}{ AB}$的长$l=\frac {30\pi ×6}{180}=\pi$
解:连接OB,
∵∠AOC=90°,∠C=15°
∴∠A=180°-90°-15°=75°
∵OA=OB
∴∠A=∠OBA=75°
∴∠AOB=180°-75°-75°=30°
∵半径OA=6
∴$\overset{\LARGE{ \frown}}{ AB}$的长$l=\frac {30\pi ×6}{180}=\pi$

解析:
连接OB。
∵OA=OB,
∴△OAB是等腰三角形,∠OAB=∠OBA。
在△AOC中,∠AOC=90°,∠C=15°,
∴∠OAC=180°-∠AOC-∠C=180°-90°-15°=75°,
∴∠OAB=∠OBA=75°,
∴∠AOB=180°-∠OAB-∠OBA=180°-75°-75°=30°。
∵OA=6,
∴$\overset{\frown}{AB}$的长为$\frac{30\pi×6}{180}=\pi$。
π
∵OA=OB,
∴△OAB是等腰三角形,∠OAB=∠OBA。
在△AOC中,∠AOC=90°,∠C=15°,
∴∠OAC=180°-∠AOC-∠C=180°-90°-15°=75°,
∴∠OAB=∠OBA=75°,
∴∠AOB=180°-∠OAB-∠OBA=180°-75°-75°=30°。
∵OA=6,
∴$\overset{\frown}{AB}$的长为$\frac{30\pi×6}{180}=\pi$。
π