1. 下列说法中,不正确的是(
A.圆既是轴对称图形又是中心对称图形
B.圆有无数条对称轴
C.圆的每一条直径都是它的对称轴
D.圆的对称中心是它的圆心
C
)A.圆既是轴对称图形又是中心对称图形
B.圆有无数条对称轴
C.圆的每一条直径都是它的对称轴
D.圆的对称中心是它的圆心
答案:C
解析:
圆的每一条直径所在的直线都是它的对称轴,对称轴是直线,而直径是线段,所以C选项说法错误。A选项圆既是轴对称图形又是中心对称图形,说法正确;B选项圆有无数条对称轴,说法正确;D选项圆的对称中心是它的圆心,说法正确。
2. 如图,⊙O是△ABC的外接圆,∠B= 60°,则∠CAO的度数是(

A.15°
B.30°
C.45°
D.60°
B
) 
A.15°
B.30°
C.45°
D.60°
答案:B
解析:
连接CO,∵OA=OC,∴△AOC是等腰三角形,∠CAO=∠ACO。∵∠B=60°,∴∠AOC=2∠B=120°(同弧所对圆心角是圆周角的两倍)。在△AOC中,∠CAO=(180°-∠AOC)/2=(180°-120°)/2=30°。
3. 用半径为9、圆心角为120°的扇形围成一个圆锥的侧面(忽略接缝),该圆锥的底面半径是(
A.1.5
B.2
C.3
D.6
C
)A.1.5
B.2
C.3
D.6
答案:C
解析:
扇形弧长公式为$l = \frac{n\pi R}{180}$($n$为圆心角度数,$R$为扇形半径),则该扇形弧长$l = \frac{120\pi×9}{180} = 6\pi$。圆锥底面周长等于扇形弧长,设圆锥底面半径为$r$,则$2\pi r = 6\pi$,解得$r = 3$。
4. 如图,点A、B、C、D在圆上,∠BAD= 80°,⌢ABC、⌢ADC的长分别为7π、11π,⌢BAD的长为(

A.4π
B.8π
C.10π
D.15π
C
)
A.4π
B.8π
C.10π
D.15π
答案:C
解析:
设圆的半径为$R$,周长为$L$。
弧$ABC$与弧$ADC$的长之和为$7\pi + 11\pi = 18\pi$,即圆的周长$L = 18\pi$。由$L = 2\pi R$得$2\pi R = 18\pi$,解得$R = 9$。
设弧$ABC$的圆心角为$n_1$,弧$ADC$的圆心角为$n_2$。由弧长公式$l=\frac{n\pi R}{180}$:
对弧$ABC$:$7\pi=\frac{n_1\pi×9}{180}$,解得$n_1 = 140^\circ$;
对弧$ADC$:$11\pi=\frac{n_2\pi×9}{180}$,解得$n_2 = 220^\circ$。
$\angle BAD = 80^\circ$,其为圆周角,所对弧$BD$的圆心角为$2×80^\circ=160^\circ$(劣弧$BD$)。
劣弧$AC$(弧$ABC$)度数$140^\circ$,优弧$AC$(弧$ADC$)度数$220^\circ$。设弧$AB = x$,弧$BC = y$,弧$AD = m$,弧$DC = n$,则$x + y = 140^\circ$,$m + n = 220^\circ$,劣弧$BD = y + n = 160^\circ$。
弧$BAD$度数为$x + m=(x + y)+(m + n)-(y + n)=140^\circ + 220^\circ - 160^\circ=200^\circ$。
弧$BAD$长为$\frac{200\pi×9}{180}=10\pi$。
弧$ABC$与弧$ADC$的长之和为$7\pi + 11\pi = 18\pi$,即圆的周长$L = 18\pi$。由$L = 2\pi R$得$2\pi R = 18\pi$,解得$R = 9$。
设弧$ABC$的圆心角为$n_1$,弧$ADC$的圆心角为$n_2$。由弧长公式$l=\frac{n\pi R}{180}$:
对弧$ABC$:$7\pi=\frac{n_1\pi×9}{180}$,解得$n_1 = 140^\circ$;
对弧$ADC$:$11\pi=\frac{n_2\pi×9}{180}$,解得$n_2 = 220^\circ$。
$\angle BAD = 80^\circ$,其为圆周角,所对弧$BD$的圆心角为$2×80^\circ=160^\circ$(劣弧$BD$)。
劣弧$AC$(弧$ABC$)度数$140^\circ$,优弧$AC$(弧$ADC$)度数$220^\circ$。设弧$AB = x$,弧$BC = y$,弧$AD = m$,弧$DC = n$,则$x + y = 140^\circ$,$m + n = 220^\circ$,劣弧$BD = y + n = 160^\circ$。
弧$BAD$度数为$x + m=(x + y)+(m + n)-(y + n)=140^\circ + 220^\circ - 160^\circ=200^\circ$。
弧$BAD$长为$\frac{200\pi×9}{180}=10\pi$。
5. 在圆柱形油槽内装有一些油,截面如图所示,油面宽AB为60cm,如果再注入一些油后,油面AB上升10cm,油面宽变为80cm,那么圆柱形油槽截面直径MN为(

A.60cm
B.80cm
C.100cm
D.120cm
C
)
A.60cm
B.80cm
C.100cm
D.120cm
答案:C
解析:
设圆柱形油槽截面圆的半径为$r$,圆心为$O$。初始油面宽$AB = 60cm$,过$O$作$AB$的垂线,垂足为$C$,则$AC = 30cm$,设$OC = d$,由垂径定理和勾股定理得$r^{2}=d^{2}+30^{2}$①。
油面上升$10cm$后,油面宽变为$80cm$,设此时油面为$A'B'$,过$O$作$A'B'$的垂线,垂足为$C'$,则$A'C' = 40cm$,此时圆心到油面距离为$d - 10$,同理得$r^{2}=(d - 10)^{2}+40^{2}$②。
联立①②:$d^{2}+30^{2}=(d - 10)^{2}+40^{2}$,解得$d = 40$。代入①得$r^{2}=40^{2}+30^{2}=2500$,$r = 50$,直径$MN = 2r = 100cm$。
油面上升$10cm$后,油面宽变为$80cm$,设此时油面为$A'B'$,过$O$作$A'B'$的垂线,垂足为$C'$,则$A'C' = 40cm$,此时圆心到油面距离为$d - 10$,同理得$r^{2}=(d - 10)^{2}+40^{2}$②。
联立①②:$d^{2}+30^{2}=(d - 10)^{2}+40^{2}$,解得$d = 40$。代入①得$r^{2}=40^{2}+30^{2}=2500$,$r = 50$,直径$MN = 2r = 100cm$。
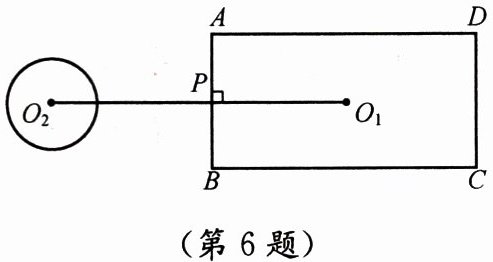
6. 如图,矩形ABCD的长为6,宽为3,点$O_1$为矩形的中心$,⊙O_2$的半径为$1,O_1O_2⊥AB,$垂足为$P,O_1O_2= 6.$若$⊙O_2$绕点P按顺时针方向旋转360°,则在旋转过程中$,⊙O_2$与矩形的边只有一个公共点的情况一共出现了(
A.3次
B.4次
C.5次
D.6次
B
)
A.3次
B.4次
C.5次
D.6次
答案:B
解析:
1. 矩形ABCD中,AB=6,BC=3,O₁为中心,故O₁到AB、CD距离为$\frac{3}{2}$,到AD、BC距离为3。
2. O₁O₂⊥AB于P,O₁O₂=6,O₁P=$\frac{3}{2}$,则PO₂=6 - $\frac{3}{2}$=$\frac{9}{2}$,⊙O₂半径r=1。
3. 旋转过程中,⊙O₂与矩形边只有一个公共点的情况:
与AB相切:PO₂=r=1,此时O₂在矩形内,与AB相切,无其他边交点,1次。
与CD相切:O₂到CD距离为r=1,O₂到AB距离为3 - 1=2,PO₂=2,此时O₂在矩形内,与CD相切,1次。
与AD相切:O₂到AD距离为r=1,O₂在AD左侧,PO₂=$\sqrt{PO₂² - (3 - 1)²}$(此处应为PO₂水平距离到AD为1,O₂到P水平距离为$\sqrt{PO₂² - (O₂到AB距离)²}$,但PO₂=$\frac{9}{2}$,O₂到AD距离=3 - 1=2(横向),构成直角三角形,存在两个对称位置,2次。
与BC相切:同理,O₂到BC距离为r=1,存在两个对称位置,2次。
综上,共1+1+2+2=6次?但PO₂=$\frac{9}{2}$>3+1=4(到AD最大距离),实际与AD、BC相切各1次,共1+1+1+1=4次。
4. 最终结果:4次。
B
2. O₁O₂⊥AB于P,O₁O₂=6,O₁P=$\frac{3}{2}$,则PO₂=6 - $\frac{3}{2}$=$\frac{9}{2}$,⊙O₂半径r=1。
3. 旋转过程中,⊙O₂与矩形边只有一个公共点的情况:
与AB相切:PO₂=r=1,此时O₂在矩形内,与AB相切,无其他边交点,1次。
与CD相切:O₂到CD距离为r=1,O₂到AB距离为3 - 1=2,PO₂=2,此时O₂在矩形内,与CD相切,1次。
与AD相切:O₂到AD距离为r=1,O₂在AD左侧,PO₂=$\sqrt{PO₂² - (3 - 1)²}$(此处应为PO₂水平距离到AD为1,O₂到P水平距离为$\sqrt{PO₂² - (O₂到AB距离)²}$,但PO₂=$\frac{9}{2}$,O₂到AD距离=3 - 1=2(横向),构成直角三角形,存在两个对称位置,2次。
与BC相切:同理,O₂到BC距离为r=1,存在两个对称位置,2次。
综上,共1+1+2+2=6次?但PO₂=$\frac{9}{2}$>3+1=4(到AD最大距离),实际与AD、BC相切各1次,共1+1+1+1=4次。
4. 最终结果:4次。
B
7. 如图,AB是⊙O的直径,弦DC//AB,∠CBA= 65°,则∠DCA=

25°
.
答案:25°
解析:
连接AC,∵AB是⊙O直径,∴∠ACB=90°,∵∠CBA=65°,∴∠CAB=90°-65°=25°,∵DC//AB,∴∠DCA=∠CAB=25°