2. 如图,在边长为 6 cm 正方形 ABCD 中,点 P 从点 A 出发,沿 AB 向点 B 以 1 cm/s 的速度移动,点 Q 从点 B 出发,沿边 BC 和 CD 向点 D 以 2 cm/s 的速度移动,点 P、Q 分别从点 A、B 同时出发,当其中一点到终点时,另一点也随之停止运动。过了
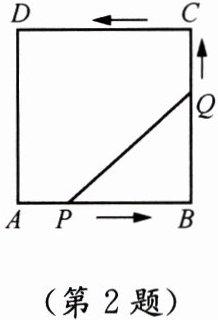
2,$\frac{10}{3}$
s 后,$\triangle PBQ$的面积等于 $8 cm^2$。
答案:2,$\frac{10}{3}$
解析:
设运动时间为$t$秒,$0\leq t\leq6$。
情况1:当$0\leq t\leq3$时,$Q$在$BC$边上
$PB=6-t$,$BQ=2t$,$\triangle PBQ$面积为$\frac{1}{2}× PB× BQ$,则:
$\frac{1}{2}(6-t)×2t=8$,化简得$t^2 - 6t + 8 = 0$,解得$t=2$或$t=4$($t=4>3$舍去),$t=2$。
情况2:当$3<t\leq6$时,$Q$在$CD$边上
$Q$坐标为$(12-2t,6)$,$\triangle PBQ$面积为$18 - 3t$,则:
$18 - 3t = 8$,解得$t=\frac{10}{3}$($3<\frac{10}{3}\leq6$,符合)。
综上,$t=2$或$t=\frac{10}{3}$。
情况1:当$0\leq t\leq3$时,$Q$在$BC$边上
$PB=6-t$,$BQ=2t$,$\triangle PBQ$面积为$\frac{1}{2}× PB× BQ$,则:
$\frac{1}{2}(6-t)×2t=8$,化简得$t^2 - 6t + 8 = 0$,解得$t=2$或$t=4$($t=4>3$舍去),$t=2$。
情况2:当$3<t\leq6$时,$Q$在$CD$边上
$Q$坐标为$(12-2t,6)$,$\triangle PBQ$面积为$18 - 3t$,则:
$18 - 3t = 8$,解得$t=\frac{10}{3}$($3<\frac{10}{3}\leq6$,符合)。
综上,$t=2$或$t=\frac{10}{3}$。
3. 如图,小岛 A 在码头 B 的正西方向,A、B 相距 40 n mile。上午 9 时,一渔船和一游艇同时出发,渔船以 20 n mile/h 的速度从码头 B 向正北方向出海作业,游艇以 25 n mile/h 的速度从岛 A 返回码头 B。一段时间后,渔船因故障停航在 C 处并发出信号。游艇在 D 处收到信号后直接向渔船驶去,上午 11 时到达 C 处。游艇是在上午何时收到信号的?(1 n mile ≈ 1.852 km)


答案:上午10时。
解析:
设游艇从出发到收到信号经过了$ t $小时,则收到信号的时间为$ 9 + t $时。从收到信号到到达C处经过的时间为$ (2 - t) $小时(总时间为11 - 9 = 2小时)。
分析各段距离:
1. 渔船行驶距离:渔船速度20 n mile/h,行驶$ t $小时后停在C处,故$ BC = 20t $ n mile。
2. 游艇从A到D的距离:游艇速度25 n mile/h,行驶$ t $小时到达D处,故$ AD = 25t $ n mile。因$ AB = 40 $ n mile,所以$ DB = AB - AD = 40 - 25t $ n mile。
3. 游艇从D到C的距离:D到C为直角三角形$ DBC $的斜边,由勾股定理得$ DC = \sqrt{DB^2 + BC^2} = \sqrt{(40 - 25t)^2 + (20t)^2} $。又因游艇从D到C速度为25 n mile/h,行驶时间$ (2 - t) $小时,故$ DC = 25(2 - t) $。
建立方程并求解:
$\sqrt{(40 - 25t)^2 + (20t)^2} = 25(2 - t)$
两边平方得:
$(40 - 25t)^2 + (20t)^2 = [25(2 - t)]^2$
展开并化简:
$1600 - 2000t + 625t^2 + 400t^2 = 625(4 - 4t + t^2)$
$1025t^2 - 2000t + 1600 = 2500 - 2500t + 625t^2$
$400t^2 + 500t - 900 = 0$
化简为:
$4t^2 + 5t - 9 = 0$
解得:
$t = \frac{-5 \pm \sqrt{25 + 144}}{8} = \frac{-5 \pm 13}{8}$
取正根$ t = 1 $。
结论:
游艇出发1小时后收到信号,即上午10时。
分析各段距离:
1. 渔船行驶距离:渔船速度20 n mile/h,行驶$ t $小时后停在C处,故$ BC = 20t $ n mile。
2. 游艇从A到D的距离:游艇速度25 n mile/h,行驶$ t $小时到达D处,故$ AD = 25t $ n mile。因$ AB = 40 $ n mile,所以$ DB = AB - AD = 40 - 25t $ n mile。
3. 游艇从D到C的距离:D到C为直角三角形$ DBC $的斜边,由勾股定理得$ DC = \sqrt{DB^2 + BC^2} = \sqrt{(40 - 25t)^2 + (20t)^2} $。又因游艇从D到C速度为25 n mile/h,行驶时间$ (2 - t) $小时,故$ DC = 25(2 - t) $。
建立方程并求解:
$\sqrt{(40 - 25t)^2 + (20t)^2} = 25(2 - t)$
两边平方得:
$(40 - 25t)^2 + (20t)^2 = [25(2 - t)]^2$
展开并化简:
$1600 - 2000t + 625t^2 + 400t^2 = 625(4 - 4t + t^2)$
$1025t^2 - 2000t + 1600 = 2500 - 2500t + 625t^2$
$400t^2 + 500t - 900 = 0$
化简为:
$4t^2 + 5t - 9 = 0$
解得:
$t = \frac{-5 \pm \sqrt{25 + 144}}{8} = \frac{-5 \pm 13}{8}$
取正根$ t = 1 $。
结论:
游艇出发1小时后收到信号,即上午10时。
如图,在 $Rt\triangle ABC$ 中,$\angle B = 90^{\circ}$,AB = 6 cm,BC = 8 cm,点 P 从点 A 出发沿 AB 向点 B 以 1 cm/s 的速度移动,与此同时,点 Q 从点 B 出发沿 BC 向点 C 以 2 cm/s 的速度移动。如果点 P、Q 分别从点 A、B 同时出发,当点 Q 运动到点 C 时,两点停止运动。
1. 经过多长时间,$\triangle PBQ$ 的面积等于 $8 cm^2$?

2. $\triangle PBQ$ 的面积会等于 $10 cm^2$吗?若会,请求出此时的运动时间。
1. 经过多长时间,$\triangle PBQ$ 的面积等于 $8 cm^2$?

2. $\triangle PBQ$ 的面积会等于 $10 cm^2$吗?若会,请求出此时的运动时间。
答案:1. 解:设经过$t$秒,$\triangle PBQ$的面积等于$8cm^2$。
已知$AP = t cm$,则$PB=(6 - t)cm$,$BQ = 2t cm$。
根据三角形面积公式$S=\frac{1}{2}ah$(这里$a = PB$,$h = BQ$),可得$\frac{1}{2}(6 - t)×2t=8$。
化简得$(6 - t)t = 8$,即$6t-t^{2}=8$,移项化为标准一元二次方程形式$t^{2}-6t + 8 = 0$。
因式分解得$(t - 2)(t - 4)=0$,则$t - 2 = 0$或$t - 4 = 0$。
解得$t_{1}=2$,$t_{2}=4$。
因为$0\leqslant t\leqslant4$(点$Q$从$B$到$C$运动时间$t=\frac{8}{2}=4s$),所以经过$2s$或$4s$,$\triangle PBQ$的面积等于$8cm^2$。
2. 解:假设$\triangle PBQ$的面积等于$10cm^2$,设运动时间为$t$秒。
同样根据面积公式$\frac{1}{2}(6 - t)×2t = 10$,化简得$(6 - t)t = 10$,即$t^{2}-6t + 10 = 0$。
对于一元二次方程$ax^{2}+bx + c = 0$(这里$a = 1$,$b=-6$,$c = 10$),判别式$\Delta=b^{2}-4ac=(-6)^{2}-4×1×10=36 - 40=-4\lt0$。
所以此方程无实数根,即$\triangle PBQ$的面积不会等于$10cm^2$。
已知$AP = t cm$,则$PB=(6 - t)cm$,$BQ = 2t cm$。
根据三角形面积公式$S=\frac{1}{2}ah$(这里$a = PB$,$h = BQ$),可得$\frac{1}{2}(6 - t)×2t=8$。
化简得$(6 - t)t = 8$,即$6t-t^{2}=8$,移项化为标准一元二次方程形式$t^{2}-6t + 8 = 0$。
因式分解得$(t - 2)(t - 4)=0$,则$t - 2 = 0$或$t - 4 = 0$。
解得$t_{1}=2$,$t_{2}=4$。
因为$0\leqslant t\leqslant4$(点$Q$从$B$到$C$运动时间$t=\frac{8}{2}=4s$),所以经过$2s$或$4s$,$\triangle PBQ$的面积等于$8cm^2$。
2. 解:假设$\triangle PBQ$的面积等于$10cm^2$,设运动时间为$t$秒。
同样根据面积公式$\frac{1}{2}(6 - t)×2t = 10$,化简得$(6 - t)t = 10$,即$t^{2}-6t + 10 = 0$。
对于一元二次方程$ax^{2}+bx + c = 0$(这里$a = 1$,$b=-6$,$c = 10$),判别式$\Delta=b^{2}-4ac=(-6)^{2}-4×1×10=36 - 40=-4\lt0$。
所以此方程无实数根,即$\triangle PBQ$的面积不会等于$10cm^2$。