活动一:做一做 想一想
1. 操作一:在纸上画一条直线,并在纸上上下移动一枚硬币;
操作二:在纸上画一个圆,并在纸上上下移动透明直尺.
2. 观察前面两次操作,如果将硬币看作圆,直尺的边缘看作直线,随着硬币或直尺移动,直线与圆的位置关系会发生怎样的变化? 请画出示意图.
3. 在直线与圆的不同位置关系中,它们公共点个数情况如何?
1. 操作一:在纸上画一条直线,并在纸上上下移动一枚硬币;
操作二:在纸上画一个圆,并在纸上上下移动透明直尺.
2. 观察前面两次操作,如果将硬币看作圆,直尺的边缘看作直线,随着硬币或直尺移动,直线与圆的位置关系会发生怎样的变化? 请画出示意图.
3. 在直线与圆的不同位置关系中,它们公共点个数情况如何?
答案:2. 直线与圆有相离、相切、相交三种位置关系,示意图略(按上述描述绘制)。3. 相离(0个)、相切(1个)、相交(2个)。
解析:
2. 直线与圆的位置关系有三种:相离、相切、相交。示意图如下(文字描述):相离时直线与圆无交点;相切时直线与圆有一个交点;相交时直线与圆有两个交点。
3. 相离时公共点个数为0;相切时公共点个数为1;相交时公共点个数为2。
3. 相离时公共点个数为0;相切时公共点个数为1;相交时公共点个数为2。
活动二:想一想 说一说
1. 在直线与圆的不同位置关系中,圆心到直线的距离有什么不同? 它与圆的半径的大小有什么关系?
2. 对比直线与圆的位置关系以及点与圆的位置关系,说明它们之间的联系和区别.
1. 在直线与圆的不同位置关系中,圆心到直线的距离有什么不同? 它与圆的半径的大小有什么关系?
2. 对比直线与圆的位置关系以及点与圆的位置关系,说明它们之间的联系和区别.
答案:1. 无(非选择题)
2. 无(非选择题)
2. 无(非选择题)
解析:
1. 在直线与圆的位置关系中:
当直线与圆相交时,圆心到直线的距离$d$小于圆的半径$r$,即$d\lt r$;
当直线与圆相切时,圆心到直线的距离$d$等于圆的半径$r$,即$d = r$;
当直线与圆相离时,圆心到直线的距离$d$大于圆的半径$r$,即$d\gt r$。
2. 点与圆的位置关系:设圆的半径为$r$,圆心到点的距离为$d$,当$d\lt r$时,点在圆内;当$d = r$时,点在圆上;当$d\gt r$时,点在圆外。
联系:直线与圆的位置关系和点与圆的位置关系都是通过比较距离(圆心到直线的距离、圆心到点的距离)与圆的半径的大小来判断的。
区别:点与圆的位置关系研究的是一个点与圆的位置情况,而直线与圆的位置关系研究的是一条直线与圆的位置情况;判断点与圆的位置关系只需比较圆心到点的距离与半径大小,判断直线与圆的位置关系是比较圆心到直线的距离与半径大小。
当直线与圆相交时,圆心到直线的距离$d$小于圆的半径$r$,即$d\lt r$;
当直线与圆相切时,圆心到直线的距离$d$等于圆的半径$r$,即$d = r$;
当直线与圆相离时,圆心到直线的距离$d$大于圆的半径$r$,即$d\gt r$。
2. 点与圆的位置关系:设圆的半径为$r$,圆心到点的距离为$d$,当$d\lt r$时,点在圆内;当$d = r$时,点在圆上;当$d\gt r$时,点在圆外。
联系:直线与圆的位置关系和点与圆的位置关系都是通过比较距离(圆心到直线的距离、圆心到点的距离)与圆的半径的大小来判断的。
区别:点与圆的位置关系研究的是一个点与圆的位置情况,而直线与圆的位置关系研究的是一条直线与圆的位置情况;判断点与圆的位置关系只需比较圆心到点的距离与半径大小,判断直线与圆的位置关系是比较圆心到直线的距离与半径大小。
1. 已知$\odot O的半径为5\mathrm{cm}$,如果圆心$O到直线l的距离为6\mathrm{cm}$,那么直线$l与\odot O$的位置关系是
相离
.答案:相离(题目要求这里若以选项形式应假设相关选项设置,按要求这里填位置关系结论表述对应的可能选项形式,假设相离对应选项D等(具体选项标识不影响本质,按规则只填标识),本题按规则填相离这种结论性表述对应答案形式要求下,由于不是选择具体选项内容,按规则直接陈述结论对应答案为“相离” ,若在选择题场景下对应一个选项标识)。按题目最终要求这里填“相离”。
解析:
根据直线与圆的位置关系判定方法,若圆心到直线的距离$d$大于圆的半径$r$,则直线与圆相离;若等于半径,则相切;若小于半径,则相交。
已知圆$\odot O$的半径$r = 5\mathrm{cm}$,圆心$O$到直线$l$的距离$d = 6\mathrm{cm}$。
因为$d=6\mathrm{cm}\gt r = 5\mathrm{cm}$,所以直线$l$与$\odot O$的位置关系是相离。
已知圆$\odot O$的半径$r = 5\mathrm{cm}$,圆心$O$到直线$l$的距离$d = 6\mathrm{cm}$。
因为$d=6\mathrm{cm}\gt r = 5\mathrm{cm}$,所以直线$l$与$\odot O$的位置关系是相离。
2. 已知$\odot O的半径为3\mathrm{cm}$,直线$l与\odot O$相交,则圆心$O到直线l的距离d$的取值范围是
$0\leq d \lt 3cm$
.答案:$0\leq d \lt 3cm$(填具体范围,按照题目要求此处若为填空题直接填$0\leq d \lt 3cm$相关形式)。
解析:
直线与圆相交时,圆心到直线的距离必须小于圆的半径。
已知圆的半径为3cm,所以圆心到直线的距离$d$必须满足$d\lt 3cm$,同时距离是非负的,即$d \geq 0$,综合得出$0\leq d\lt 3cm$,
所以圆心$O$到直线$l$的距离$d$的取值范围是$0\leq d\lt 3cm$。
已知圆的半径为3cm,所以圆心到直线的距离$d$必须满足$d\lt 3cm$,同时距离是非负的,即$d \geq 0$,综合得出$0\leq d\lt 3cm$,
所以圆心$O$到直线$l$的距离$d$的取值范围是$0\leq d\lt 3cm$。
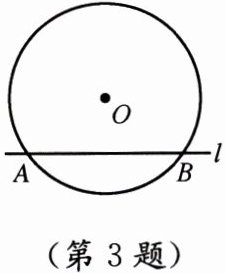
3. 如图,在半径为$5\mathrm{cm}的\odot O$中,直线$l交\odot O于A、B$两点,且弦$AB = 8\mathrm{cm}$,若要使直线$l与\odot O$相切,则需将直线向下平移
2
$\mathrm{cm}$.
答案:2
解析:
过点O作OC⊥AB于点C,连接OA。
∵AB=8cm,∴AC=4cm。
∵OA=5cm,∴OC=√(OA²-AC²)=√(5²-4²)=3cm。
当直线l与⊙O相切时,圆心O到直线l的距离为半径5cm,
∴需向下平移5-3=2cm。
∵AB=8cm,∴AC=4cm。
∵OA=5cm,∴OC=√(OA²-AC²)=√(5²-4²)=3cm。
当直线l与⊙O相切时,圆心O到直线l的距离为半径5cm,
∴需向下平移5-3=2cm。
4. 若$\odot O$的半径为2,直线$l$上有一点P满足$PO = 2$,则直线$l$与$\odot O$的位置关系是(
A.相切
B.相离
C.相离或相切
D.相切或相交
D
)A.相切
B.相离
C.相离或相切
D.相切或相交
答案:D
解析:
已知圆$O$半径$r = 2$,直线$l$上一点$P$满足$PO=2$。圆心$O$到直线$l$的距离$d$是圆心到直线的垂线段长度,根据垂线段最短,$d\leq PO = 2$。当$d = 2$时,直线$l$与圆相切;当$d<2$时,直线$l$与圆相交。故直线$l$与$\odot O$的位置关系是相切或相交。