4. 甲、乙、丙 3 家工厂在广告中都宣称,自己的某种电子产品的使用寿命是 8 年,质量检测部门从这 3 家工厂销售的产品中各抽查了 10 件,统计实际使用寿命如下(单位:年):
甲厂:4,5,5,5,5,7,9,12,13,15;乙厂:3,3,4,5,6,8,8,8,10,11;丙厂:3,4,4,4,7,9,10,11,11,12.
根据上述统计结果,请回答下列问题:
(1) 分别求出三组数据的平均数、中位数、众数.
(2) 这 3 家工厂的推销广告分别利用了哪一种表示“集中趋势”的特征数据?
(3) 如果你是顾客,会选购哪家工厂的产品? 为什么?
甲厂:4,5,5,5,5,7,9,12,13,15;乙厂:3,3,4,5,6,8,8,8,10,11;丙厂:3,4,4,4,7,9,10,11,11,12.
根据上述统计结果,请回答下列问题:
(1) 分别求出三组数据的平均数、中位数、众数.
(2) 这 3 家工厂的推销广告分别利用了哪一种表示“集中趋势”的特征数据?
(3) 如果你是顾客,会选购哪家工厂的产品? 为什么?
答案:(1)甲厂:平均数:$(4+5+5+5+5+7+9+12+13+15)÷10=8$;中位数:$(5+7)÷2=6$;众数:5。
乙厂:平均数:$(3+3+4+5+6+8+8+8+10+11)÷10=6.6$;中位数:$(6+8)÷2=7$;众数:8。
丙厂:平均数:$(3+4+4+4+7+9+10+11+11+12)÷10=7.5$;中位数:$(7+9)÷2=8$;众数:4。
(2)甲厂:平均数;乙厂:众数;丙厂:中位数。
(3)选购丙厂的产品。因为丙厂的中位数是8,说明有一半以上的产品使用寿命达到或超过8年,且数据整体分布较稳定,多数产品寿命较长。
乙厂:平均数:$(3+3+4+5+6+8+8+8+10+11)÷10=6.6$;中位数:$(6+8)÷2=7$;众数:8。
丙厂:平均数:$(3+4+4+4+7+9+10+11+11+12)÷10=7.5$;中位数:$(7+9)÷2=8$;众数:4。
(2)甲厂:平均数;乙厂:众数;丙厂:中位数。
(3)选购丙厂的产品。因为丙厂的中位数是8,说明有一半以上的产品使用寿命达到或超过8年,且数据整体分布较稳定,多数产品寿命较长。
1. 一组数据由 5 个正整数组成,中位数是 3,众数是 7 且唯一,则这 5 个正整数的平均数是
4
.答案:4
解析:
将5个正整数从小到大排列为$a,b,c,d,e$,中位数是3,故$c=3$。众数是7且唯一,7只能在$d,e$中($a,b\leq3$),则$d=7,e=7$(7至少出现2次)。$a,b$为正整数且$a\leq b\leq3$,为保证7唯一众数,$a,b$需不同且不为3(避免3出现次数≥2),故$a=1,b=2$。数据为1,2,3,7,7,平均数为$(1+2+3+7+7)÷5=4$。
2. 小华所在的九年级(1)班共有 50 名学生,一次体检测量了全班学生的身高,由此求得该班学生的平均身高为 1.65 m,而小华的身高为 1.66 m. 下列说法中,错误的是 (
A.1.65 m 是该班学生身高的平均水平
B.班上比小华高的学生不会超过 25 人
C.这组身高的中位数不一定是 1.65 m
D.这组身高的众数不一定是 1.65 m
B
)A.1.65 m 是该班学生身高的平均水平
B.班上比小华高的学生不会超过 25 人
C.这组身高的中位数不一定是 1.65 m
D.这组身高的众数不一定是 1.65 m
答案:B
解析:
A选项:平均身高为1.65m,表示所有学生身高总和除以人数,因此能代表该班学生身高的平均水平,说法正确。
B选项:班上比小华高的学生人数是否超过25人与数据分布情况有关,平均数无法限制具体分布,因此无法确定比小华高的学生人数一定不超过25人,说法错误。
C选项:中位数是将数据从小到大排列后位于中间的值,或中间两数的平均值,与平均数无必然联系,因此中位数不一定是1.65m,说法正确。
D选项:众数是数据中出现次数最多的数,与平均数无必然联系,因此众数不一定是1.65m,说法正确。
B选项:班上比小华高的学生人数是否超过25人与数据分布情况有关,平均数无法限制具体分布,因此无法确定比小华高的学生人数一定不超过25人,说法错误。
C选项:中位数是将数据从小到大排列后位于中间的值,或中间两数的平均值,与平均数无必然联系,因此中位数不一定是1.65m,说法正确。
D选项:众数是数据中出现次数最多的数,与平均数无必然联系,因此众数不一定是1.65m,说法正确。
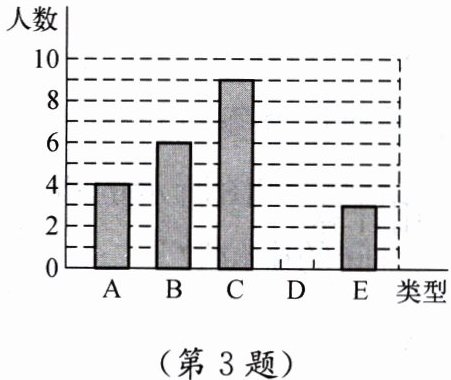
3. 某单位 750 名职工积极参加捐书活动. 现采用随机抽样的方法抽取 30 名职工,对他们的捐书数量进行统计,统计结果共有 4 本、5 本、6 本、7 本、8 本五类,分别用 A、B、C、D、E 表示,根据统计数据绘制成了如图所示的不完整的条形统计图. 根据图中给出的信息解答下列问题:
(1) 补全条形统计图;
(2) 求这 30 名职工捐书数量的平均数、众数和中位数;
(3) 估计该单位 750 名职工共捐书多少本.
]
(1) 补全条形统计图;
(2) 求这 30 名职工捐书数量的平均数、众数和中位数;
(3) 估计该单位 750 名职工共捐书多少本.
]

答案:(1) 补全条形统计图(D对应8人)。
(2) 平均数6本;众数6本;中位数6本。
(3) 4500本。
(2) 平均数6本;众数6本;中位数6本。
(3) 4500本。
解析:
(1)从条形统计图中可知A(4本)有4人,B(5本)有6人,C(6本)有9人(原统计图高度对应9),E(8本)有3人。
所以D(7本)的人数为$30 - 4 - 6 - 9 - 3 = 8$人。
补全条形统计图:在D对应的条形上画高度到8人的位置。
(2)
平均数:$\bar{x}=\frac{4× 4 + 5× 6+6× 9 + 7× 8+8× 3}{30}=\frac{16 + 30+54 + 56+24}{30}=\frac{180}{30}=6$(本)。
众数:6本出现的次数最多,为9次,所以众数是6本。
中位数:将30个数据从小到大排列,第15、16个数据都是6本,所以中位数是6本。
(3)$750×6 = 4500$(本)。
所以D(7本)的人数为$30 - 4 - 6 - 9 - 3 = 8$人。
补全条形统计图:在D对应的条形上画高度到8人的位置。
(2)
平均数:$\bar{x}=\frac{4× 4 + 5× 6+6× 9 + 7× 8+8× 3}{30}=\frac{16 + 30+54 + 56+24}{30}=\frac{180}{30}=6$(本)。
众数:6本出现的次数最多,为9次,所以众数是6本。
中位数:将30个数据从小到大排列,第15、16个数据都是6本,所以中位数是6本。
(3)$750×6 = 4500$(本)。