1. 对甲、乙两人的 5 次数学测验成绩进行统计,得出两人 5 次测验成绩数据的平均数均为 90,方差分别是 $s^2_{甲}= 51$、$s^2_{乙}= 12$. 成绩比较稳定的是
乙
(填“甲”或“乙”).答案:乙
解析:
方差是衡量数据波动大小的量,方差越小,数据越稳定。已知$s^2_{甲}=51$,$s^2_{乙}=12$,因为$12\lt51$,即$s^2_{乙}\lt s^2_{甲}$,所以乙的成绩波动较小,乙的成绩比较稳定。
2. 已知一组数据为 2,0,$-1$,3,$-4$,则这组数据的方差为
6
.答案:6(题目是填空题,按照要求这里应填方差的结果数值)
解析:
先计算这组数据的平均数:
$\bar{x}=\frac{2 + 0+(-1)+3+(-4)}{5}=\frac{2 - 1+3 - 4}{5}=0$
再根据方差公式$s^{2}=\frac{1}{n}[(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+\cdots+(x_{n}-\bar{x})^{2}]$计算方差:
$s^{2}=\frac{1}{5}[(2 - 0)^{2}+(0 - 0)^{2}+(-1 - 0)^{2}+(3 - 0)^{2}+(-4 - 0)^{2}]$
$=\frac{1}{5}(4 + 0+1 + 9+16)$
$=\frac{1}{5}×30 = 6$
$\bar{x}=\frac{2 + 0+(-1)+3+(-4)}{5}=\frac{2 - 1+3 - 4}{5}=0$
再根据方差公式$s^{2}=\frac{1}{n}[(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+\cdots+(x_{n}-\bar{x})^{2}]$计算方差:
$s^{2}=\frac{1}{5}[(2 - 0)^{2}+(0 - 0)^{2}+(-1 - 0)^{2}+(3 - 0)^{2}+(-4 - 0)^{2}]$
$=\frac{1}{5}(4 + 0+1 + 9+16)$
$=\frac{1}{5}×30 = 6$
3. 已知一组数据 0,1,2,$x$,5 的极差是 7,则这组数据中的 $x$ 为
7或-2
.答案:7或-2
解析:
极差是一组数据中最大值与最小值的差。已知数据0,1,2,x,5的极差是7。
若x是最大值,则x - 0 = 7,解得x = 7;
若x是最小值,则5 - x = 7,解得x = -2。
综上,x为7或-2。
若x是最大值,则x - 0 = 7,解得x = 7;
若x是最小值,则5 - x = 7,解得x = -2。
综上,x为7或-2。
4. 一组数据的方差 $s^2= \frac{1}{15}[(x_1 - 10)^2 + (x_2 - 10)^2 + … + (x_n - 10)^2]$,则这组数据的平均数是
10
,$n= $15
.答案:平均数是$10$,$n = 15$(按照题目顺序,答案依次为$10$;$15$)
解析:
方差的计算公式为$s^2=\frac{1}{n}[(x_1-\bar{x})^2+(x_2 - \bar{x})^2+\cdots+(x_n - \bar{x})^2]$,其中$\bar{x}$表示这组数据的平均数,$n$表示数据的个数。
已知方差$s^2 = \frac{1}{15}[(x_1 - 10)^2 + (x_2 - 10)^2 + \cdots + (x_n - 10)^2]$,与方差计算公式对比可得,这组数据的平均数$\bar{x}=10$,数据个数$n = 15$。
已知方差$s^2 = \frac{1}{15}[(x_1 - 10)^2 + (x_2 - 10)^2 + \cdots + (x_n - 10)^2]$,与方差计算公式对比可得,这组数据的平均数$\bar{x}=10$,数据个数$n = 15$。
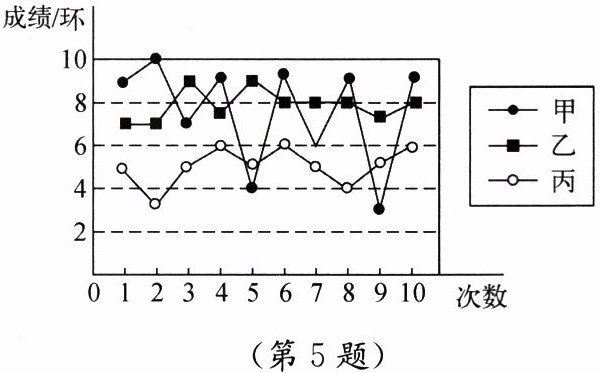
5. 甲、乙、丙三人各射击 10 次的成绩(单位:环)如图,射击成绩最稳定的是(
A.甲
B.乙
C.丙
D.无法判断
B
)
A.甲
B.乙
C.丙
D.无法判断
答案:B
解析:
观察折线图,乙的成绩波动最小,方差最小,成绩最稳定。
6. 某中学开展演讲比赛,九年级(1)班、九年级(2)班根据初赛成绩各选出 5 名选手参加复赛,两个班各选出的 5 名选手的复赛成绩(满分为 100 分)如图所示.
(1)分别求出两班复赛的平均成绩和方差;
(2)根据(1)的计算结果,分析两个班级的复赛成绩.

(1)分别求出两班复赛的平均成绩和方差;
(2)根据(1)的计算结果,分析两个班级的复赛成绩.

答案:(1)九年级(1)班复赛成绩:85,100,80,85,100
平均成绩:$\bar{x}_1=\frac{85+100+80+85+100}{5}=90$(分)
方差:$s_1^2=\frac{(85-90)^2+(100-90)^2+(80-90)^2+(85-90)^2+(100-90)^2}{5}=\frac{25+100+100+25+100}{5}=70$
九年级(2)班复赛成绩:70,75,100,75,80
平均成绩:$\bar{x}_2=\frac{70+75+100+75+80}{5}=80$(分)
方差:$s_2^2=\frac{(70-80)^2+(75-80)^2+(100-80)^2+(75-80)^2+(80-80)^2}{5}=\frac{100+25+400+25+0}{5}=110$
(2)九年级(1)班平均成绩高于九年级(2)班,说明(1)班整体成绩较好;九年级(1)班方差小于(2)班,说明(1)班成绩更稳定。
平均成绩:$\bar{x}_1=\frac{85+100+80+85+100}{5}=90$(分)
方差:$s_1^2=\frac{(85-90)^2+(100-90)^2+(80-90)^2+(85-90)^2+(100-90)^2}{5}=\frac{25+100+100+25+100}{5}=70$
九年级(2)班复赛成绩:70,75,100,75,80
平均成绩:$\bar{x}_2=\frac{70+75+100+75+80}{5}=80$(分)
方差:$s_2^2=\frac{(70-80)^2+(75-80)^2+(100-80)^2+(75-80)^2+(80-80)^2}{5}=\frac{100+25+400+25+0}{5}=110$
(2)九年级(1)班平均成绩高于九年级(2)班,说明(1)班整体成绩较好;九年级(1)班方差小于(2)班,说明(1)班成绩更稳定。
1. 已知一组数据 $-3$,$x$,$-2$,3,16 的中位数为 1,其方差为
46.8
.答案:46.8
解析:
将数据排序,因中位数为1且数据个数为5,故排序后第3个数为1,可得x=1。数据为-3,-2,1,3,16。平均数$\bar{x}=\frac{-3-2+1+3+16}{5}=3$。方差$s^2=\frac{(-3-3)^2+(-2-3)^2+(1-3)^2+(3-3)^2+(16-3)^2}{5}=\frac{36+25+4+0+169}{5}=46.8$。
2. 若一组数据 1,7,8,$a$,4 的平均数是 5,中位数是 $m$,极差是 $n$,则 $m + n= $
12
.答案:12
解析:
1. 根据平均数的定义,有:
$\frac{1 + 7 + 8 + a + 4}{5} = 5$,
解得$a = 5$,
将数据从小到大排序:$1, 4, 5, 7, 8$,
中位数$m = 5$,
极差$n = 8 - 1 = 7$,
所以$m + n = 5 + 7 = 12$。
$\frac{1 + 7 + 8 + a + 4}{5} = 5$,
解得$a = 5$,
将数据从小到大排序:$1, 4, 5, 7, 8$,
中位数$m = 5$,
极差$n = 8 - 1 = 7$,
所以$m + n = 5 + 7 = 12$。
3. 在某中学举行的演讲比赛中,九年级 5 名参赛选手的成绩部分如下表所示,已知这 5 名选手的平均成绩为 91 分,根据表中的数据,这 5 名选手成绩的方差为(

A.2
B.6.8
C.34
D.93
B
)
A.2
B.6.8
C.34
D.93
答案:1. 首先求$3$号选手的成绩:
设$3$号选手成绩为$x$分。
根据平均数公式$\bar{x}=\frac{x_{1} + x_{2}+\cdots+x_{n}}{n}$(这里$n = 5$,$\bar{x}=91$),可得$\frac{90 + 95+x + 89+88}{5}=91$。
化简方程:$90 + 95+x + 89+88 = 91×5$。
计算左边$90 + 95+89+88+x=(90 + 95)+(89 + 88)+x=185+177+x=362+x$,右边$91×5 = 455$。
则$362+x = 455$,解得$x = 455−362=93$。
2. 然后求方差:
根据方差公式$s^{2}=\frac{1}{n}[(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+\cdots+(x_{n}-\bar{x})^{2}]$。
已知$n = 5$,$\bar{x}=91$,$x_{1}=90$,$x_{2}=95$,$x_{3}=93$,$x_{4}=89$,$x_{5}=88$。
$(x_{1}-\bar{x})^{2}=(90 - 91)^{2}=(-1)^{2}=1$;$(x_{2}-\bar{x})^{2}=(95 - 91)^{2}=4^{2}=16$;$(x_{3}-\bar{x})^{2}=(93 - 91)^{2}=2^{2}=4$;$(x_{4}-\bar{x})^{2}=(89 - 91)^{2}=(-2)^{2}=4$;$(x_{5}-\bar{x})^{2}=(88 - 91)^{2}=(-3)^{2}=9$。
$s^{2}=\frac{1×(1 + 16+4 + 4+9)}{5}=\frac{34}{5}=6.8$。
所以这$5$名选手成绩的方差为$6.8$,答案是B。
设$3$号选手成绩为$x$分。
根据平均数公式$\bar{x}=\frac{x_{1} + x_{2}+\cdots+x_{n}}{n}$(这里$n = 5$,$\bar{x}=91$),可得$\frac{90 + 95+x + 89+88}{5}=91$。
化简方程:$90 + 95+x + 89+88 = 91×5$。
计算左边$90 + 95+89+88+x=(90 + 95)+(89 + 88)+x=185+177+x=362+x$,右边$91×5 = 455$。
则$362+x = 455$,解得$x = 455−362=93$。
2. 然后求方差:
根据方差公式$s^{2}=\frac{1}{n}[(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+\cdots+(x_{n}-\bar{x})^{2}]$。
已知$n = 5$,$\bar{x}=91$,$x_{1}=90$,$x_{2}=95$,$x_{3}=93$,$x_{4}=89$,$x_{5}=88$。
$(x_{1}-\bar{x})^{2}=(90 - 91)^{2}=(-1)^{2}=1$;$(x_{2}-\bar{x})^{2}=(95 - 91)^{2}=4^{2}=16$;$(x_{3}-\bar{x})^{2}=(93 - 91)^{2}=2^{2}=4$;$(x_{4}-\bar{x})^{2}=(89 - 91)^{2}=(-2)^{2}=4$;$(x_{5}-\bar{x})^{2}=(88 - 91)^{2}=(-3)^{2}=9$。
$s^{2}=\frac{1×(1 + 16+4 + 4+9)}{5}=\frac{34}{5}=6.8$。
所以这$5$名选手成绩的方差为$6.8$,答案是B。
解析:
设3号选手成绩为$x$分,根据平均成绩为91分,可列方程:
$\frac{90 + 95 + x + 89 + 88}{5} = 91$,
$90 + 95 + x + 89 + 88 = 91×5$,
$362+x=455$,
$x = 93$,
方差$S^{2}=\frac{1}{5}×[(90 - 91)^{2}+(95 - 91)^{2}+(93 - 91)^{2}+(89 - 91)^{2}+(88 - 91)^{2}]$
$=\frac{1}{5}×[(-1)^{2}+4^{2}+2^{2}+(-2)^{2}+(-3)^{2}]$
$=\frac{1}{5}×(1 + 16 + 4 + 4 + 9)$
$=\frac{1}{5}×34$
$ = 6.8$
$\frac{90 + 95 + x + 89 + 88}{5} = 91$,
$90 + 95 + x + 89 + 88 = 91×5$,
$362+x=455$,
$x = 93$,
方差$S^{2}=\frac{1}{5}×[(90 - 91)^{2}+(95 - 91)^{2}+(93 - 91)^{2}+(89 - 91)^{2}+(88 - 91)^{2}]$
$=\frac{1}{5}×[(-1)^{2}+4^{2}+2^{2}+(-2)^{2}+(-3)^{2}]$
$=\frac{1}{5}×(1 + 16 + 4 + 4 + 9)$
$=\frac{1}{5}×34$
$ = 6.8$