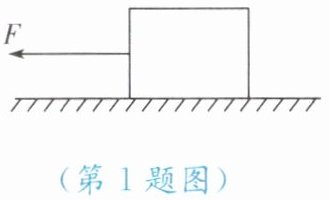
1. 如图所示,用水平拉力 $ F $ 拉着重为 $ 100 \, N $ 的物体在水平地面上向左匀速移动了 $ 5 \, m $,物体所受地面的摩擦力大小为 $ 20 \, N $,则(
A.重力做的功是 $ 500 \, J $
B.拉力大小为 $ 100 \, N $
C.拉力大小为 $ 120 \, N $
D.拉力做的功为 $ 100 \, J $
D
)
A.重力做的功是 $ 500 \, J $
B.拉力大小为 $ 100 \, N $
C.拉力大小为 $ 120 \, N $
D.拉力做的功为 $ 100 \, J $
答案:1. 首先分析物体的受力情况:
因为物体在水平地面上匀速移动,根据二力平衡条件,在水平方向上,拉力$F$与摩擦力$f$是一对平衡力,即$F = f$。
已知$f = 20N$,所以$F = 20N$,故B、C错误。
2. 然后分析重力做功情况:
根据功的计算公式$W=Fs$(其中$F$是力,$s$是在力的方向上移动的距离),重力$G = 100N$,物体在重力方向(竖直方向)上没有移动距离,即$h = 0$。
那么重力做的功$W_G=Gh=100N×0 = 0J$,故A错误。
3. 最后分析拉力做功情况:
已知拉力$F = 20N$,物体在拉力方向(水平方向)上移动的距离$s = 5m$。
根据功的计算公式$W = Fs$,可得拉力做的功$W_F=Fs=20N×5m = 100J$。
综上,答案是D。
因为物体在水平地面上匀速移动,根据二力平衡条件,在水平方向上,拉力$F$与摩擦力$f$是一对平衡力,即$F = f$。
已知$f = 20N$,所以$F = 20N$,故B、C错误。
2. 然后分析重力做功情况:
根据功的计算公式$W=Fs$(其中$F$是力,$s$是在力的方向上移动的距离),重力$G = 100N$,物体在重力方向(竖直方向)上没有移动距离,即$h = 0$。
那么重力做的功$W_G=Gh=100N×0 = 0J$,故A错误。
3. 最后分析拉力做功情况:
已知拉力$F = 20N$,物体在拉力方向(水平方向)上移动的距离$s = 5m$。
根据功的计算公式$W = Fs$,可得拉力做的功$W_F=Fs=20N×5m = 100J$。
综上,答案是D。
2. 以下事例中重力做功的是(
A.冰球在水平的冰面上滚动
B.皮划艇在平静水面上快速滑行
C.跳水运动员下落
D.举重运动员举着杠铃静止不动
C
)A.冰球在水平的冰面上滚动
B.皮划艇在平静水面上快速滑行
C.跳水运动员下落
D.举重运动员举着杠铃静止不动
答案:C
3. 一个人先后用同样大小的力沿水平方向拉木箱,使木箱分别在光滑和粗糙两种不同的水平地面上前进相同的距离。关于拉力所做的功,下列说法中正确的是(
A.在粗糙地面上做功较多
B.在光滑地面上做功较多
C.两次做功一样多
D.条件不够,无法比较两次做功的多少
C
)A.在粗糙地面上做功较多
B.在光滑地面上做功较多
C.两次做功一样多
D.条件不够,无法比较两次做功的多少
答案:C
4. 李壮用 $ 10 \, N $ 的水平拉力使重 $ 300 \, N $ 的箱子沿水平地面移动了 $ 5 \, m $,张强将这个箱子匀速举高 $ 2 \, m $,王明举着这个箱子在空中停留了 $ 5 \, s $。李壮做功
50
$ J $,张强做功600
$ J $,王明使箱子在空中停留 $ 5 \, s $ 的过程中做功0
$ J $。答案:50
600
0
600
0
5. 一辆重为 $ 2 × 10^{4} \, N $ 的汽车在水平的公路上匀速行驶,汽车所受的阻力为车重的 $ 0.3 $ 倍,汽车在 $ 1 \, min $ 内行驶 $ 1.5 \, km $。在 $ 1 \, min $ 内牵引力做功多少焦?汽车的重力做功多少焦?
答案:解:$W=Fs={ 0.3×2×10^4 } \text{N}×{ 1500 } \text{m}={9×10^6 } \text{J}$
重力做功为0
重力做功为0
6. 如图所示,在拉力 $ F $ 作用下,重为 $ 120 \, N $ 的物体竖直向上做匀速直线运动,物体上升的速度为 $ 0.4 \, m/s $。拉力 $ F $ 的大小是多少牛?在 $ 5 \, s $ 内拉力做了多少功?(不计动滑轮和绳子的重力以及各处的摩擦)


答案:解:$F=\frac 13G=\frac 13×120\ \text {N}=40\ \text {N}$
$ W=Fs=Gh=120\ \text {N}×0.4\ \text {m/s}×5\ \text {s}=240\ \text {J}$
$ W=Fs=Gh=120\ \text {N}×0.4\ \text {m/s}×5\ \text {s}=240\ \text {J}$