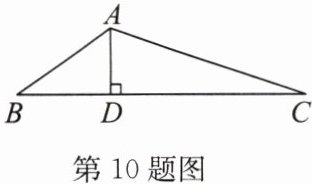
10.(2025·上海期中)如图,在△ABC 中,∠BAC = 126°,AD ⊥ BC 于点 D,且 AB + BD = DC,那么∠C 的度数是
18°
.
答案:18°
解析:
解:在DC上截取DE=BD,连接AE。
∵AD⊥BC,DE=BD,
∴AB=AE,∠B=∠AEB。
设∠C=x,
∵AB+BD=DC,DE=BD,
∴AE=EC,
∴∠EAC=∠C=x,
∴∠AEB=∠EAC+∠C=2x,
∴∠B=2x。
在△ABC中,∠BAC+∠B+∠C=180°,
∵∠BAC=126°,
∴126°+2x+x=180°,
解得x=18°,
即∠C=18°。
18°
∵AD⊥BC,DE=BD,
∴AB=AE,∠B=∠AEB。
设∠C=x,
∵AB+BD=DC,DE=BD,
∴AE=EC,
∴∠EAC=∠C=x,
∴∠AEB=∠EAC+∠C=2x,
∴∠B=2x。
在△ABC中,∠BAC+∠B+∠C=180°,
∵∠BAC=126°,
∴126°+2x+x=180°,
解得x=18°,
即∠C=18°。
18°
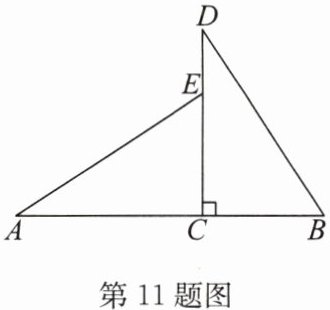
11.(12 分)如图,C 为 AB 上一点,CD ⊥ AB,点 E 在 CD 上,连接 BD,AE,BC = EC,AC = DC.
求证:△ACE ≌ △DCB.
求证:△ACE ≌ △DCB.

答案:证明:
∵CD⊥AB,
∴∠ACE=∠DCB=90°.
在△ACE和△DCB中,{AC=DC,∠ACE=∠DCB,EC=BC,
∴△ACE≌△DCB(SAS).
∵CD⊥AB,
∴∠ACE=∠DCB=90°.
在△ACE和△DCB中,{AC=DC,∠ACE=∠DCB,EC=BC,
∴△ACE≌△DCB(SAS).
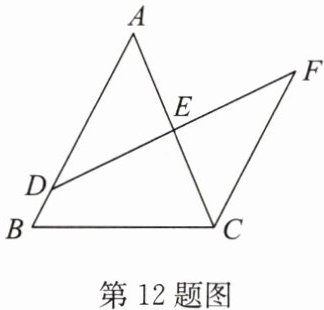
12.(12 分)(2024·泰州兴化期末)如图,D 是 AB 上一点,DF 交 AC 于点 E,AB // FC,AD = FC,求证:DE = EF.

答案:证明:
∵AB//FC,
∴∠A=∠ECF,∠ADE=∠F.
又
∵AD=CF,
∴△ADE≌△CFE(ASA).
∴DE=EF.
∵AB//FC,
∴∠A=∠ECF,∠ADE=∠F.
又
∵AD=CF,
∴△ADE≌△CFE(ASA).
∴DE=EF.
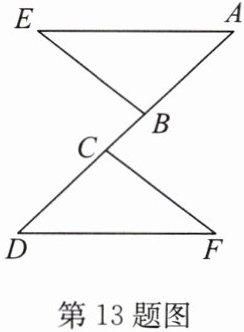
13.(12 分)如图,点 A,B,C,D 在同一条直线上,AC = BD,AE = DF,AE // DF. 求证:∠E = ∠F.

答案:证明:
∵AE//DF,
∴∠A=∠D.
∵AC=BD,
∴AC-BC=BD-BC,即AB=CD.
在△ABE和△DCF中,{AE=DF,∠A=∠D,AB=DC,
∴△ABE≌△DCF(SAS).
∴∠E=∠F.
∵AE//DF,
∴∠A=∠D.
∵AC=BD,
∴AC-BC=BD-BC,即AB=CD.
在△ABE和△DCF中,{AE=DF,∠A=∠D,AB=DC,
∴△ABE≌△DCF(SAS).
∴∠E=∠F.
14.(14 分)如图,在△ABC 中,AD 是△ABC 的角平分线,P 是线段 AD 上的一个动点,PE ⊥ AD 交直线 BC 于点 E.
(1)若∠B = 30°,∠ACB = 80°,求∠E 的度数;
(2)当点 P 在线段 AD 上运动时,若∠E 是锐角,请求出∠E,∠ACB,∠B 之间的关系.
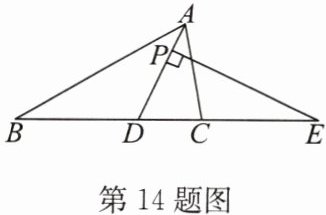
(1)若∠B = 30°,∠ACB = 80°,求∠E 的度数;
(2)当点 P 在线段 AD 上运动时,若∠E 是锐角,请求出∠E,∠ACB,∠B 之间的关系.

答案:解:
(1)
∵∠B=30°,∠ACB=80°,
∴∠BAC=180°-∠B-∠ACB=70°.
∵AD是△ABC的角平分线,
∴∠BAD=1/2∠BAC=35°.
∴∠PDE=∠B+∠BAD=65°.
∵PE⊥AD,
∴∠E=90°-∠PDE=25°.
(2)
∵AD是△ABC的角平分线,
∴∠BAD=1/2∠BAC=1/2(180°-∠B-∠ACB).
∴∠PDE=∠B+∠BAD=∠B+1/2(180°-∠B-∠ACB).
∵PE⊥AD,
∴∠E=90°-∠PDE=90°-[∠B+1/2(180°-∠B-∠ACB)]=1/2(∠ACB-∠B).
(1)
∵∠B=30°,∠ACB=80°,
∴∠BAC=180°-∠B-∠ACB=70°.
∵AD是△ABC的角平分线,
∴∠BAD=1/2∠BAC=35°.
∴∠PDE=∠B+∠BAD=65°.
∵PE⊥AD,
∴∠E=90°-∠PDE=25°.
(2)
∵AD是△ABC的角平分线,
∴∠BAD=1/2∠BAC=1/2(180°-∠B-∠ACB).
∴∠PDE=∠B+∠BAD=∠B+1/2(180°-∠B-∠ACB).
∵PE⊥AD,
∴∠E=90°-∠PDE=90°-[∠B+1/2(180°-∠B-∠ACB)]=1/2(∠ACB-∠B).