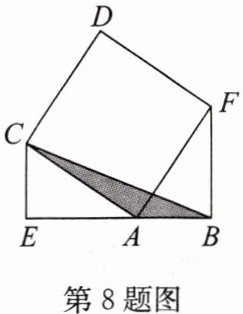
8. 如图,四边形$ACDF$是正方形,$\angle CEA和\angle ABF都是直角且E$,$A$,$B$三点共线,若$AB = 4$,则阴影部分的面积是
8
.
答案:8
解析:
证明:
∵ 四边形 $ACDF$ 是正方形,
∴ $AC = AF$,$\angle CAF = 90°$,
∵ $\angle CEA = \angle ABF = 90°$,$E$,$A$,$B$ 共线,
∴ $\angle EAC + \angle FAB = 90°$,$\angle EAC + \angle ECA = 90°$,
∴ $\angle ECA = \angle FAB$,
在 $\triangle CEA$ 和 $\triangle ABF$ 中,
$\begin{cases} \angle CEA = \angle ABF \\\angle ECA = \angle FAB \\AC = FA \end{cases}$,
∴ $\triangle CEA \cong \triangle ABF$(AAS),
∴ $EA = BF$,$CE = AB = 4$,
设 $EA = x$,则 $BF = x$,$EB = EA + AB = x + 4$,
阴影部分面积 $S_{\triangle CAB} = \frac{1}{2} × AB × CE = \frac{1}{2} × 4 × 4 = 8$。
8
∵ 四边形 $ACDF$ 是正方形,
∴ $AC = AF$,$\angle CAF = 90°$,
∵ $\angle CEA = \angle ABF = 90°$,$E$,$A$,$B$ 共线,
∴ $\angle EAC + \angle FAB = 90°$,$\angle EAC + \angle ECA = 90°$,
∴ $\angle ECA = \angle FAB$,
在 $\triangle CEA$ 和 $\triangle ABF$ 中,
$\begin{cases} \angle CEA = \angle ABF \\\angle ECA = \angle FAB \\AC = FA \end{cases}$,
∴ $\triangle CEA \cong \triangle ABF$(AAS),
∴ $EA = BF$,$CE = AB = 4$,
设 $EA = x$,则 $BF = x$,$EB = EA + AB = x + 4$,
阴影部分面积 $S_{\triangle CAB} = \frac{1}{2} × AB × CE = \frac{1}{2} × 4 × 4 = 8$。
8
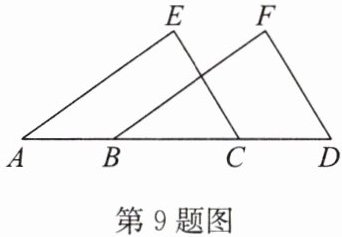
9. 如图,点$A$,$B$,$C$,$D$在同一条直线上,$AE // BF$,$AE = BF$. 若
①或③
,则$AB = CD$. 请从①$CE // DF$;②$CE = DF$;③$\angle E = \angle F这3$个选项中选择一个作为条件(写序号),使结论成立,并说明理由.
答案:解:选①,理由如下:
∵AE//BF,CE//DF,
∴∠A=∠FBD,∠ACE=∠D.又
∵AE=BF,
∴△ACE≌△BDF(AAS).
∴AC=BD.
∴AC-BC=BD-BC,即AB=CD.
选③,理由如下:
∵AE//BF,
∴∠A=∠FBD.又
∵AE=BF,∠E=∠F,
∴△ACE≌△BDF(ASA).
∴AC=BD.
∴AC-BC=BD-BC,即AB=CD.
∵AE//BF,CE//DF,
∴∠A=∠FBD,∠ACE=∠D.又
∵AE=BF,
∴△ACE≌△BDF(AAS).
∴AC=BD.
∴AC-BC=BD-BC,即AB=CD.
选③,理由如下:
∵AE//BF,
∴∠A=∠FBD.又
∵AE=BF,∠E=∠F,
∴△ACE≌△BDF(ASA).
∴AC=BD.
∴AC-BC=BD-BC,即AB=CD.
10. 如图,在$\triangle ABC$中,$\angle B = \angle C$,点$D$,$E$,$F分别在边AB$,$BC$,$AC$上,且$BD = CE$,$\angle DEF = \angle C$. 请找出图中的全等三角形,并证明你的结论.
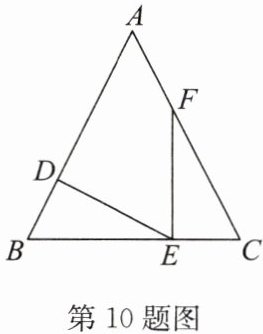

答案:解:△BDE≌△CEF.证明如下:
∵∠DEF=∠C,∠FEB=∠C+∠EFC=∠DEF+∠BED,
∴∠DEB=∠CFE.在△BDE和△CEF中,∠B=∠C,∠DEB=∠EFC,BD=CE,
∴△BDE≌△CEF(AAS).
∵∠DEF=∠C,∠FEB=∠C+∠EFC=∠DEF+∠BED,
∴∠DEB=∠CFE.在△BDE和△CEF中,∠B=∠C,∠DEB=∠EFC,BD=CE,
∴△BDE≌△CEF(AAS).
11. 如图,在四边形$ABCD$中,点$E在边AD$上,其中$\angle BAE = \angle BCE = \angle ACD = 90^{\circ}$,且$BC = CE$. 求证:$AC = DC$.
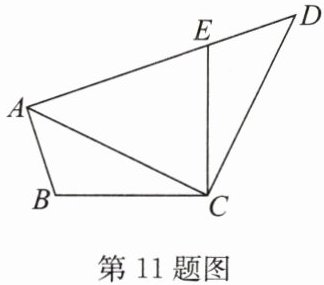

答案:证明:
∵∠BCE=∠ACD=90°,
∴∠BCA+∠ACE=∠ACE+∠DCE,
∴∠BCA=∠DCE.在△ACD中,∠ACD=90°,
∴∠CAE+∠D=90°.
∵∠BAE=∠BAC+∠CAE=90°,
∴∠BAC=∠D.在△ABC和△DEC中,∠BAC=∠D,∠BCA=∠ECD,BC=EC,
∴△ABC≌△DEC(AAS),
∴AC=DC.
∵∠BCE=∠ACD=90°,
∴∠BCA+∠ACE=∠ACE+∠DCE,
∴∠BCA=∠DCE.在△ACD中,∠ACD=90°,
∴∠CAE+∠D=90°.
∵∠BAE=∠BAC+∠CAE=90°,
∴∠BAC=∠D.在△ABC和△DEC中,∠BAC=∠D,∠BCA=∠ECD,BC=EC,
∴△ABC≌△DEC(AAS),
∴AC=DC.