1. 下列条件中,不能判定△ABC是等腰三角形的是(
A.$a = 3$,$b = 3$,$c = 4$
B.$a:b:c = 2:3:4$
C.$∠B = 50^{\circ}$,$∠C = 80^{\circ}$
D.$∠A:∠B:∠C = 1:1:2$
B
)A.$a = 3$,$b = 3$,$c = 4$
B.$a:b:c = 2:3:4$
C.$∠B = 50^{\circ}$,$∠C = 80^{\circ}$
D.$∠A:∠B:∠C = 1:1:2$
答案：B
解析：
A. $a = 3$, $b = 3$, $c = 4$，有两边相等，是等腰三角形；
B. $a:b:c = 2:3:4$，三边均不相等，不是等腰三角形；
C. $\angle B = 50°$, $\angle C = 80°$，则$\angle A=180° - 50° - 80°=50°$，$\angle A=\angle B$，是等腰三角形；
D. $\angle A:\angle B:\angle C = 1:1:2$，设$\angle A=x$, $\angle B=x$, $\angle C=2x$，$x+x+2x=180°$，$x=45°$，$\angle A=\angle B=45°$，是等腰三角形。
B
B. $a:b:c = 2:3:4$，三边均不相等，不是等腰三角形；
C. $\angle B = 50°$, $\angle C = 80°$，则$\angle A=180° - 50° - 80°=50°$，$\angle A=\angle B$，是等腰三角形；
D. $\angle A:\angle B:\angle C = 1:1:2$，设$\angle A=x$, $\angle B=x$, $\angle C=2x$，$x+x+2x=180°$，$x=45°$，$\angle A=\angle B=45°$，是等腰三角形。
B
2. 如图,在四边形ABCD中,$AD// BC$,BE平分$∠ABC$交AD于点E. 若$AB = 7$,$AD = 9$,则$DE= $
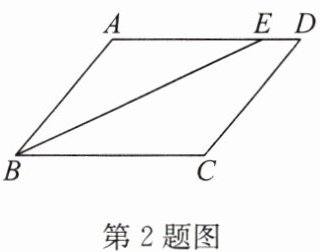
2
.答案：2
解析：
解：
∵ $AD // BC$，
∴ $\angle AEB = \angle EBC$（两直线平行，内错角相等）。
∵ $BE$ 平分 $\angle ABC$，
∴ $\angle ABE = \angle EBC$。
∴ $\angle ABE = \angle AEB$，
∴ $\triangle ABE$ 为等腰三角形，$AE = AB$。
∵ $AB = 7$，
∴ $AE = 7$。
∵ $AD = 9$，
∴ $DE = AD - AE = 9 - 7 = 2$。
2
∵ $AD // BC$，
∴ $\angle AEB = \angle EBC$（两直线平行，内错角相等）。
∵ $BE$ 平分 $\angle ABC$，
∴ $\angle ABE = \angle EBC$。
∴ $\angle ABE = \angle AEB$，
∴ $\triangle ABE$ 为等腰三角形，$AE = AB$。
∵ $AB = 7$，
∴ $AE = 7$。
∵ $AD = 9$，
∴ $DE = AD - AE = 9 - 7 = 2$。
2
3. 如图,在△ABC中,$∠ABC和∠ACB$的平分线交于点E,过点E作$MN// BC$交AB于点M,交AC于点N. 若$BM + CN = 9$,则线段MN的长为
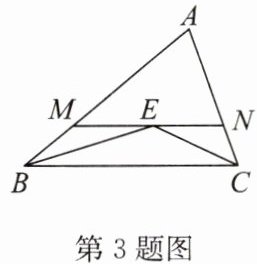
9
.答案：9
解析：
证明：
∵BE平分∠ABC，
∴∠MBE=∠EBC．
∵MN//BC，
∴∠MEB=∠EBC．
∴∠MBE=∠MEB．
∴ME=BM．
同理可证：NE=CN．
∵MN=ME+NE，
∴MN=BM+CN=9．
9
∵BE平分∠ABC，
∴∠MBE=∠EBC．
∵MN//BC，
∴∠MEB=∠EBC．
∴∠MBE=∠MEB．
∴ME=BM．
同理可证：NE=CN．
∵MN=ME+NE，
∴MN=BM+CN=9．
9
4. 如图,在△ABC中,点E在AB上,点D在BC上,$BD = BE$,$∠BAD = ∠BCE$,AD与CE相交于点F.
(1)求证：$BA = BC$；
(2)求证：△AFC为等腰三角形.
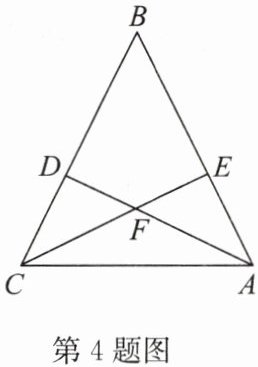
(1)求证：$BA = BC$；
(2)求证：△AFC为等腰三角形.
答案：证明:
(1)在△BCE和△BAD中,∠B=∠B,∠BCE=∠BAD,BE=BD,
∴△BCE≌△BAD(AAS).
∴BA=BC.
(2)
∵BA=BC,
∴∠BCA=∠BAC,
∴∠BCA - ∠BCE=∠BAC - ∠BAD,即∠FCA=∠FAC.
∴FA=FC,
∴△AFC为等腰三角形.
(1)在△BCE和△BAD中,∠B=∠B,∠BCE=∠BAD,BE=BD,
∴△BCE≌△BAD(AAS).
∴BA=BC.
(2)
∵BA=BC,
∴∠BCA=∠BAC,
∴∠BCA - ∠BCE=∠BAC - ∠BAD,即∠FCA=∠FAC.
∴FA=FC,
∴△AFC为等腰三角形.
5. 如图所示的图形中等腰三角形的个数是(
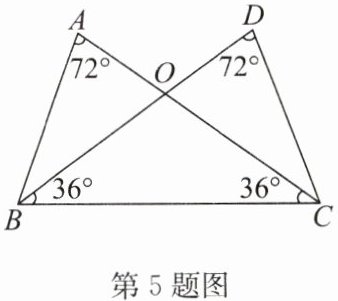
A.4
B.5
C.3
D.2
B
)A.4
B.5
C.3
D.2
答案：B
解析：
证明：在△ABC中，∠A=72°，∠B=∠C=36°，
∴AB=AC，△ABC是等腰三角形。
在△DBC中，∠D=72°，∠B=∠C=36°，
∴DB=DC，△DBC是等腰三角形。
在△ABO中，∠A=72°，∠ABO=36°，∠AOB=180°-72°-36°=72°，
∴∠A=∠AOB，AB=BO，△ABO是等腰三角形。
在△DCO中，∠D=72°，∠DCO=36°，∠DOC=180°-72°-36°=72°，
∴∠D=∠DOC，DC=CO，△DCO是等腰三角形。
在△BOC中，∠OBC=∠OCB=36°，
∴OB=OC，△BOC是等腰三角形。
综上，等腰三角形共有5个。
答案：B
∴AB=AC，△ABC是等腰三角形。
在△DBC中，∠D=72°，∠B=∠C=36°，
∴DB=DC，△DBC是等腰三角形。
在△ABO中，∠A=72°，∠ABO=36°，∠AOB=180°-72°-36°=72°，
∴∠A=∠AOB，AB=BO，△ABO是等腰三角形。
在△DCO中，∠D=72°，∠DCO=36°，∠DOC=180°-72°-36°=72°，
∴∠D=∠DOC，DC=CO，△DCO是等腰三角形。
在△BOC中，∠OBC=∠OCB=36°，
∴OB=OC，△BOC是等腰三角形。
综上，等腰三角形共有5个。
答案：B
6. 如图,在△ABC中,$∠BAC = 105^{\circ}$,$AD⊥BC$,垂足为D,若$AB + BD = CD$,则$∠B$的度数为(
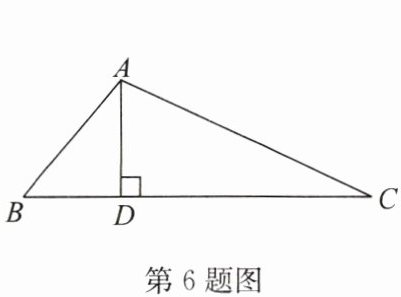
A.$20^{\circ}$
B.$25^{\circ}$
C.$45^{\circ}$
D.$50^{\circ}$
D
)A.$20^{\circ}$
B.$25^{\circ}$
C.$45^{\circ}$
D.$50^{\circ}$
答案：D
解析：
证明：在DC上截取DE=DB，连接AE。
∵AD⊥BC，DE=DB，
∴AB=AE，∠B=∠AEB。
设∠B=x，则∠AEB=x。
∵AB+BD=CD，DE=DB，
∴AE+DE=CD。
∵CD=DE+EC，
∴AE=EC，
∴∠EAC=∠C。
∵∠AEB=∠EAC+∠C，
∴∠C= $\frac{x}{2}$。
在△ABC中，∠BAC+∠B+∠C=180°，
即105°+x+$\frac{x}{2}$=180°，
解得x=50°，即∠B=50°。
D
∵AD⊥BC，DE=DB，
∴AB=AE，∠B=∠AEB。
设∠B=x，则∠AEB=x。
∵AB+BD=CD，DE=DB，
∴AE+DE=CD。
∵CD=DE+EC，
∴AE=EC，
∴∠EAC=∠C。
∵∠AEB=∠EAC+∠C，
∴∠C= $\frac{x}{2}$。
在△ABC中，∠BAC+∠B+∠C=180°，
即105°+x+$\frac{x}{2}$=180°，
解得x=50°，即∠B=50°。
D
7. 如图,在$3×3$的正方形网格中,点A,B在格点上,要找一个格点C,使△ABC是以AB为腰的等腰三角形,则图中符合条件的格点有
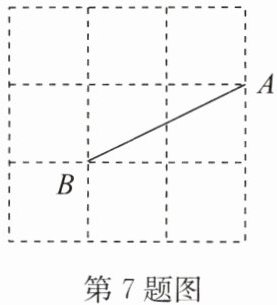
5
个.答案：5
解析：
以点A为圆心，AB长为半径画圆，与格点交于3个点；以点B为圆心，AB长为半径画圆，与格点交于2个点，其中重合1个点。符合条件的格点共有3+2-1=4个。
1
1