7. 如果一个直角三角形斜边上的中线与斜边所成的锐角为 $ 50° $,那么这个直角三角形的较小内角的度数为
25°
.答案:25°
解析:
在直角三角形中,斜边上的中线等于斜边的一半,设直角三角形为$Rt\triangle ABC$,$\angle C=90^{\circ}$,斜边$AB$的中线为$CD$,则$CD=\frac{1}{2}AB$,$AD=BD=CD$,所以$\triangle ADC$和$\triangle BDC$为等腰三角形。
已知斜边上的中线$CD$与斜边$AB$所成的锐角为$50^{\circ}$,即$\angle ADC = 50^{\circ}$或$\angle BDC=50^{\circ}$。
当$\angle ADC = 50^{\circ}$时,$\angle A=\frac{180^{\circ}-\angle ADC}{2}=\frac{180^{\circ}-50^{\circ}}{2}=65^{\circ}$,则$\angle B=90^{\circ}-\angle A=90^{\circ}-65^{\circ}=25^{\circ}$。
当$\angle BDC = 50^{\circ}$时,$\angle B=\frac{180^{\circ}-\angle BDC}{2}=\frac{180^{\circ}-50^{\circ}}{2}=65^{\circ}$,则$\angle A=90^{\circ}-\angle B=90^{\circ}-65^{\circ}=25^{\circ}$。
综上,这个直角三角形的较小内角的度数为$25^{\circ}$。
$25^{\circ}$
已知斜边上的中线$CD$与斜边$AB$所成的锐角为$50^{\circ}$,即$\angle ADC = 50^{\circ}$或$\angle BDC=50^{\circ}$。
当$\angle ADC = 50^{\circ}$时,$\angle A=\frac{180^{\circ}-\angle ADC}{2}=\frac{180^{\circ}-50^{\circ}}{2}=65^{\circ}$,则$\angle B=90^{\circ}-\angle A=90^{\circ}-65^{\circ}=25^{\circ}$。
当$\angle BDC = 50^{\circ}$时,$\angle B=\frac{180^{\circ}-\angle BDC}{2}=\frac{180^{\circ}-50^{\circ}}{2}=65^{\circ}$,则$\angle A=90^{\circ}-\angle B=90^{\circ}-65^{\circ}=25^{\circ}$。
综上,这个直角三角形的较小内角的度数为$25^{\circ}$。
$25^{\circ}$
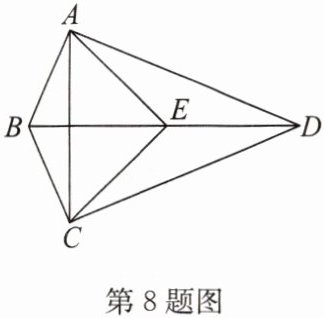
8. 如图,已知 $ \angle BAD = \angle BCD = 90° $,$ E $ 为 $ BD $ 的中点,$ BD = 4 $,$ \angle ADC = 45° $,则 $ S_{\triangle ACE} = $
2
.
答案:2
解析:
证明:
∵ $\angle BAD = 90°$,$E$ 为 $BD$ 中点,$BD = 4$,
∴ $AE = \frac{1}{2}BD = 2$(直角三角形斜边中线等于斜边一半)。
同理,$\angle BCD = 90°$,得 $CE = \frac{1}{2}BD = 2$。
设 $\angle ADB = \alpha$,则 $\angle ABD = 90° - \alpha$。
∵ $AE = BE$,
∴ $\angle BAE = \angle ABD = 90° - \alpha$,
∴ $\angle AEB = 180° - 2(90° - \alpha) = 2\alpha$。
设 $\angle CDB = \beta$,则 $\angle CBD = 90° - \beta$。
∵ $CE = BE$,
∴ $\angle BCE = \angle CBD = 90° - \beta$,
∴ $\angle CEB = 180° - 2(90° - \beta) = 2\beta$。
∵ $\angle ADC = 45°$,$\angle ADB + \angle CDB = \angle ADC$,
∴ $\alpha + \beta = 45°$,故 $\angle AEC = \angle AEB + \angle CEB = 2\alpha + 2\beta = 90°$。
∴ $S_{\triangle ACE} = \frac{1}{2} \cdot AE \cdot CE \cdot \sin \angle AEC = \frac{1}{2} × 2 × 2 × \sin 90° = 2$。
2
∵ $\angle BAD = 90°$,$E$ 为 $BD$ 中点,$BD = 4$,
∴ $AE = \frac{1}{2}BD = 2$(直角三角形斜边中线等于斜边一半)。
同理,$\angle BCD = 90°$,得 $CE = \frac{1}{2}BD = 2$。
设 $\angle ADB = \alpha$,则 $\angle ABD = 90° - \alpha$。
∵ $AE = BE$,
∴ $\angle BAE = \angle ABD = 90° - \alpha$,
∴ $\angle AEB = 180° - 2(90° - \alpha) = 2\alpha$。
设 $\angle CDB = \beta$,则 $\angle CBD = 90° - \beta$。
∵ $CE = BE$,
∴ $\angle BCE = \angle CBD = 90° - \beta$,
∴ $\angle CEB = 180° - 2(90° - \beta) = 2\beta$。
∵ $\angle ADC = 45°$,$\angle ADB + \angle CDB = \angle ADC$,
∴ $\alpha + \beta = 45°$,故 $\angle AEC = \angle AEB + \angle CEB = 2\alpha + 2\beta = 90°$。
∴ $S_{\triangle ACE} = \frac{1}{2} \cdot AE \cdot CE \cdot \sin \angle AEC = \frac{1}{2} × 2 × 2 × \sin 90° = 2$。
2
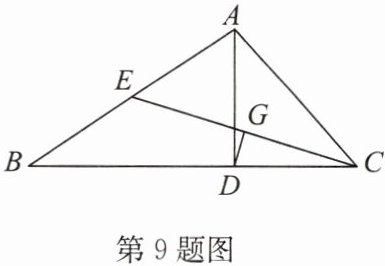
9. 如图,在 $ \triangle ABC $ 中,$ AD $ 是边 $ BC $ 上的高,$ CE $ 是边 $ AB $ 上的中线,$ G $ 是 $ CE $ 的中点,$ AB = 2CD $,求证:$ DG \perp CE $.

答案:证明:连接DE,
∵AD是边BC上的高,CE是边AB上的中线,
∴AD⊥BD,E是边AB的中点,
∴DE=$\frac{1}{2}$AB.
∵AB=2CD,
∴CD=$\frac{1}{2}$AB,
∴CD=DE,
∵G是CE的中点,
∴DG⊥CE;
∵AD是边BC上的高,CE是边AB上的中线,
∴AD⊥BD,E是边AB的中点,
∴DE=$\frac{1}{2}$AB.
∵AB=2CD,
∴CD=$\frac{1}{2}$AB,
∴CD=DE,
∵G是CE的中点,
∴DG⊥CE;
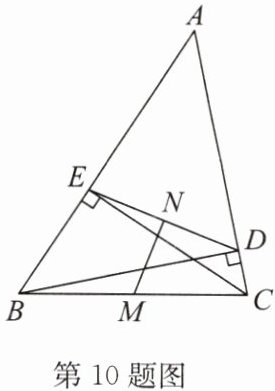
10. 如图,在 $ \triangle ABC $ 中,$ BD \perp AC $ 于点 $ D $,$ CE \perp AB $ 于点 $ E $,$ M $,$ N $ 分别是 $ BC $,$ DE $ 的中点.
(1) 求证:$ MN \perp DE $;
(2) 若 $ \angle ECB + \angle DBC = 45° $,$ DE = 10 $,求 $ MN $ 的长.
(1) 求证:$ MN \perp DE $;
(2) 若 $ \angle ECB + \angle DBC = 45° $,$ DE = 10 $,求 $ MN $ 的长.

答案:
(1)证明:如答图,连接MD,ME.
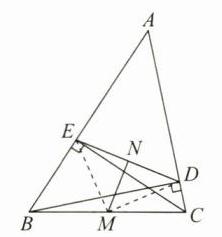
∵BD⊥AC,CE⊥AB,M是BC的中点,
∴ME=$\frac{1}{2}$BC,MD=$\frac{1}{2}$BC,
∴ME=MD.又
∵N是DE的中点,
∴MN⊥DE.
(2)解:
∵M是Rt△BEC斜边BC的中点,
∴ME=$\frac{1}{2}$BC=MC,
∴∠MEC=∠MCE;同理∠MBD=∠MDB.
∵∠ECB+∠DBC=45°,
∴∠BME+∠DMC=2(∠ECB+∠DBC)=90°,
∴∠DME=90°,又
∵N是DE的中点,
∴MN=$\frac{1}{2}$DE=$\frac{1}{2}$×10=5.
(1)证明:如答图,连接MD,ME.

∵BD⊥AC,CE⊥AB,M是BC的中点,
∴ME=$\frac{1}{2}$BC,MD=$\frac{1}{2}$BC,
∴ME=MD.又
∵N是DE的中点,
∴MN⊥DE.
(2)解:
∵M是Rt△BEC斜边BC的中点,
∴ME=$\frac{1}{2}$BC=MC,
∴∠MEC=∠MCE;同理∠MBD=∠MDB.
∵∠ECB+∠DBC=45°,
∴∠BME+∠DMC=2(∠ECB+∠DBC)=90°,
∴∠DME=90°,又
∵N是DE的中点,
∴MN=$\frac{1}{2}$DE=$\frac{1}{2}$×10=5.