9. 如图,在 $ Rt \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ AB = 5 cm $,$ AC = 3 cm $,动点 $ P $ 从点 $ B $ 出发,沿射线 $ BC $ 以 $ 2 cm/s $ 的速度移动,设运动的时间为 $ t s $. 当 $ t = $

2或$\frac{25}{8}$
时,$ \triangle ABP $ 为直角三角形.
答案:2或$\frac{25}{8}$
解析:
解:在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,$AB=5\ cm$,$AC=3\ cm$,由勾股定理得$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{5^{2}-3^{2}}=4\ cm$。
动点$P$从点$B$出发,沿射线$BC$以$2\ cm/s$的速度移动,运动时间为$t\ s$,则$BP=2t\ cm$,$PC=|BP-BC|=|2t-4|\ cm$。
$\triangle ABP$为直角三角形分两种情况:
①当$\angle APB=90^{\circ}$时,点$P$与点$C$重合,此时$BP=BC=4\ cm$,则$2t=4$,解得$t=2$。
②当$\angle BAP=90^{\circ}$时,在$Rt\triangle APC$中,$AP^{2}=AC^{2}+PC^{2}=3^{2}+(2t-4)^{2}$;在$Rt\triangle ABP$中,$AP^{2}=BP^{2}-AB^{2}=(2t)^{2}-5^{2}$。
所以$3^{2}+(2t-4)^{2}=(2t)^{2}-5^{2}$,即$9 + 4t^{2}-16t + 16=4t^{2}-25$,化简得$-16t + 25=-25$,解得$t=\frac{25}{8}$。
综上,$t=2$或$\frac{25}{8}$。
$2$或$\frac{25}{8}$
动点$P$从点$B$出发,沿射线$BC$以$2\ cm/s$的速度移动,运动时间为$t\ s$,则$BP=2t\ cm$,$PC=|BP-BC|=|2t-4|\ cm$。
$\triangle ABP$为直角三角形分两种情况:
①当$\angle APB=90^{\circ}$时,点$P$与点$C$重合,此时$BP=BC=4\ cm$,则$2t=4$,解得$t=2$。
②当$\angle BAP=90^{\circ}$时,在$Rt\triangle APC$中,$AP^{2}=AC^{2}+PC^{2}=3^{2}+(2t-4)^{2}$;在$Rt\triangle ABP$中,$AP^{2}=BP^{2}-AB^{2}=(2t)^{2}-5^{2}$。
所以$3^{2}+(2t-4)^{2}=(2t)^{2}-5^{2}$,即$9 + 4t^{2}-16t + 16=4t^{2}-25$,化简得$-16t + 25=-25$,解得$t=\frac{25}{8}$。
综上,$t=2$或$\frac{25}{8}$。
$2$或$\frac{25}{8}$
10. 如图,在四边形 $ ABCD $ 中,$ \angle ABC = \angle ADC = 90^{\circ} $,$ E $ 是对角线 $ AC $ 的中点,$ F $ 是对角线 $ BD $ 上的动点,连接 $ EF $. 若 $ AC = 6 $,$ BD = 4 $,则 $ EF $ 的最小值为

$\sqrt{5}$
.
答案:$\sqrt{5}$
解析:
证明:连接BE,DE。
∵∠ABC=∠ADC=90°,E是AC中点,AC=6,
∴BE=DE=1/2AC=3。
∴点F在BD上,当EF⊥BD时,EF最小。
∵BD=4,
∴BF=FD=2。
在Rt△BEF中,BE=3,BF=2,
∴EF=√(BE²-BF²)=√(3²-2²)=√5。
√5
∵∠ABC=∠ADC=90°,E是AC中点,AC=6,
∴BE=DE=1/2AC=3。
∴点F在BD上,当EF⊥BD时,EF最小。
∵BD=4,
∴BF=FD=2。
在Rt△BEF中,BE=3,BF=2,
∴EF=√(BE²-BF²)=√(3²-2²)=√5。
√5
11. (2024·宿城期末)如图,在 $ Rt \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ BC > AC $.
(1)请用尺规作图法,在 $ BC $ 边上求作一点 $ P $,使 $ \angle PAB = \angle B $;(保留作图痕迹,不写作法)
(2)若 $ AC = 12 $,$ BC = 18 $,求 $ \triangle PAB $ 的面积.

(1)请用尺规作图法,在 $ BC $ 边上求作一点 $ P $,使 $ \angle PAB = \angle B $;(保留作图痕迹,不写作法)
(2)若 $ AC = 12 $,$ BC = 18 $,求 $ \triangle PAB $ 的面积.

答案:
(1)如答图,点P即为所求.

(2)设CP=x,则BP=18−x.
∵∠PAB=∠B,
∴PA=PB=18−x.
在Rt△APC中,∠C=90°,由勾股定理得$PC^{2}+AC^{2}=PA^{2}$,即$x^{2}+12^{2}=(18-x)^{2},$
解得x=5,
∴BP=18−5=13.
∴S△PAB=$\frac{1}{2}$×13×12=78.
(1)如答图,点P即为所求.

(2)设CP=x,则BP=18−x.
∵∠PAB=∠B,
∴PA=PB=18−x.
在Rt△APC中,∠C=90°,由勾股定理得$PC^{2}+AC^{2}=PA^{2}$,即$x^{2}+12^{2}=(18-x)^{2},$
解得x=5,
∴BP=18−5=13.
∴S△PAB=$\frac{1}{2}$×13×12=78.
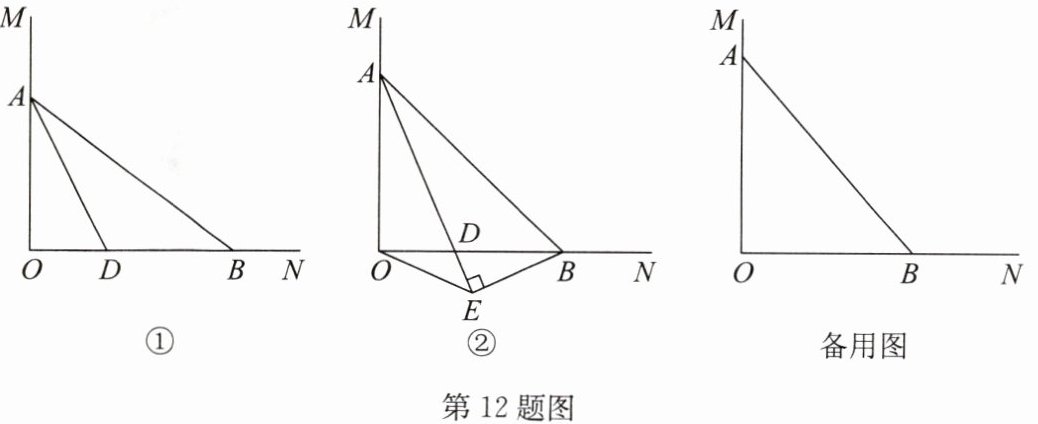
12. 已知 $ \angle MON = 90^{\circ} $,有一根长为 10 的木棒 $ AB $ 的两个端点 $ A $,$ B $ 分别在射线 $ OM $,$ ON $ 上滑动,$ \angle OAB $ 的平分线 $ AD $ 交 $ OB $ 于点 $ D $.
(1)如图①,若 $ OA = 6 $,则 $ OB = $______,$ OD = $______;
(2)如图②,过点 $ B $ 作 $ BE \perp AD $,交 $ AD $ 的延长线于点 $ E $,连接 $ OE $,在 $ AB $ 滑动的过程中,猜想线段 $ OE $,$ BE $ 有何数量关系,并说明理由;
(3)在 $ AB $ 滑动的过程中,$ \triangle AOB $ 面积的最大值为______.
]
(1)如图①,若 $ OA = 6 $,则 $ OB = $______,$ OD = $______;
(2)如图②,过点 $ B $ 作 $ BE \perp AD $,交 $ AD $ 的延长线于点 $ E $,连接 $ OE $,在 $ AB $ 滑动的过程中,猜想线段 $ OE $,$ BE $ 有何数量关系,并说明理由;
(3)在 $ AB $ 滑动的过程中,$ \triangle AOB $ 面积的最大值为______.
]

答案:
(1)8 3
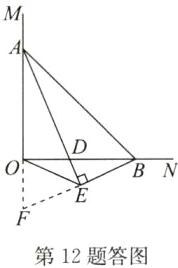
(2)解:OE=BE;理由:如答图,延长AO和BE,交于点F,则∠AEB=∠AEF=∠BOF=90°,
又
∵AD平分∠OAB,
∴∠EAF=∠EAB.
又
∵AE=AE,
∴△AEB≌△AEF(ASA),
∴BE=EF;又
∵∠BOF=90°,
∴OE=$\frac{1}{2}$BF=BE.
(3)25
(1)8 3
(2)解:OE=BE;理由:如答图,延长AO和BE,交于点F,则∠AEB=∠AEF=∠BOF=90°,
又
∵AD平分∠OAB,
∴∠EAF=∠EAB.
又
∵AE=AE,
∴△AEB≌△AEF(ASA),
∴BE=EF;又
∵∠BOF=90°,
∴OE=$\frac{1}{2}$BF=BE.

(3)25