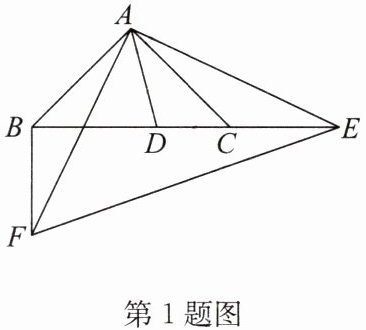
1. 如图,在 $Rt\triangle ABC$ 中,$AB = AC$,$\angle BAC = 90^{\circ}$,点 $D$,$E$ 分别在边 $BC$ 及其延长线上,$BD^{2}+CE^{2}= DE^{2}$,$F$ 为 $\triangle ABC$ 外一点,且 $FB\perp BC$,$FA\perp AE$。有下列结论：①$AF = AE$；②$\angle DAE = 45^{\circ}$；③$S_{\triangle ADE}= \frac{1}{4}AD\cdot EF$；④$CE^{2} + BE^{2}= 2AE^{2}$,其中,正确的是(
A.①②③④
B.①②④
C.①③④
D.①②
A
)A.①②③④
B.①②④
C.①③④
D.①②
答案：A
解析：
证明：
① $AF = AE$
∵ $AB = AC$, $\angle BAC = 90°$,
∴ $\angle ABC = \angle ACB = 45°$.
∵ $FB \perp BC$,
∴ $\angle FBC = 90°$, $\angle ABF = \angle FBC - \angle ABC = 45°$,
∴ $\angle ABF = \angle ACE$.
∵ $FA \perp AE$,
∴ $\angle FAE = 90° = \angle BAC$,
∴ $\angle FAB = \angle EAC$.
在 $\triangle ABF$ 和 $\triangle ACE$ 中：
$\begin{cases}\angle FAB = \angle EAC \\AB = AC \\\angle ABF = \angle ACE\end{cases}$
∴ $\triangle ABF \cong \triangle ACE$ (ASA),
∴ $AF = AE$.
② $\angle DAE = 45°$
由①得 $BF = CE$,
∵ $BD^2 + CE^2 = DE^2$,
∴ $BD^2 + BF^2 = DE^2$.
∵ $\angle FBD = 90°$,
∴ $FD^2 = BD^2 + BF^2 = DE^2$,
∴ $FD = DE$.
在 $\triangle AFD$ 和 $\triangle AED$ 中：
$\begin{cases}AF = AE \\AD = AD \\FD = DE\end{cases}$
∴ $\triangle AFD \cong \triangle AED$ (SSS),
∴ $\angle FAD = \angle EAD$.
∵ $\angle FAE = 90°$,
∴ $\angle DAE = \frac{1}{2}\angle FAE = 45°$.
③ $S_{\triangle ADE} = \frac{1}{4}AD \cdot EF$
由①得 $AF = AE$, $\angle FAE = 90°$,
∴ $\triangle AEF$ 为等腰直角三角形, $EF = \sqrt{2}AE$, 设 $AD$ 与 $EF$ 交于点 $O$, 则 $AD \perp EF$, $AO = \frac{1}{2}EF$.
$S_{\triangle ADE} = \frac{1}{2}AD \cdot AO = \frac{1}{2}AD \cdot \frac{1}{2}EF = \frac{1}{4}AD \cdot EF$.
④ $CE^2 + BE^2 = 2AE^2$
由①得 $BF = CE$, 在 $Rt\triangle BFE$ 中, $BF^2 + BE^2 = EF^2$,
∴ $CE^2 + BE^2 = EF^2$.
∵ $\triangle AEF$ 为等腰直角三角形, $EF^2 = AE^2 + AF^2 = 2AE^2$,
∴ $CE^2 + BE^2 = 2AE^2$.
综上, ①②③④均正确.
答案：A
① $AF = AE$
∵ $AB = AC$, $\angle BAC = 90°$,
∴ $\angle ABC = \angle ACB = 45°$.
∵ $FB \perp BC$,
∴ $\angle FBC = 90°$, $\angle ABF = \angle FBC - \angle ABC = 45°$,
∴ $\angle ABF = \angle ACE$.
∵ $FA \perp AE$,
∴ $\angle FAE = 90° = \angle BAC$,
∴ $\angle FAB = \angle EAC$.
在 $\triangle ABF$ 和 $\triangle ACE$ 中：
$\begin{cases}\angle FAB = \angle EAC \\AB = AC \\\angle ABF = \angle ACE\end{cases}$
∴ $\triangle ABF \cong \triangle ACE$ (ASA),
∴ $AF = AE$.
② $\angle DAE = 45°$
由①得 $BF = CE$,
∵ $BD^2 + CE^2 = DE^2$,
∴ $BD^2 + BF^2 = DE^2$.
∵ $\angle FBD = 90°$,
∴ $FD^2 = BD^2 + BF^2 = DE^2$,
∴ $FD = DE$.
在 $\triangle AFD$ 和 $\triangle AED$ 中：
$\begin{cases}AF = AE \\AD = AD \\FD = DE\end{cases}$
∴ $\triangle AFD \cong \triangle AED$ (SSS),
∴ $\angle FAD = \angle EAD$.
∵ $\angle FAE = 90°$,
∴ $\angle DAE = \frac{1}{2}\angle FAE = 45°$.
③ $S_{\triangle ADE} = \frac{1}{4}AD \cdot EF$
由①得 $AF = AE$, $\angle FAE = 90°$,
∴ $\triangle AEF$ 为等腰直角三角形, $EF = \sqrt{2}AE$, 设 $AD$ 与 $EF$ 交于点 $O$, 则 $AD \perp EF$, $AO = \frac{1}{2}EF$.
$S_{\triangle ADE} = \frac{1}{2}AD \cdot AO = \frac{1}{2}AD \cdot \frac{1}{2}EF = \frac{1}{4}AD \cdot EF$.
④ $CE^2 + BE^2 = 2AE^2$
由①得 $BF = CE$, 在 $Rt\triangle BFE$ 中, $BF^2 + BE^2 = EF^2$,
∴ $CE^2 + BE^2 = EF^2$.
∵ $\triangle AEF$ 为等腰直角三角形, $EF^2 = AE^2 + AF^2 = 2AE^2$,
∴ $CE^2 + BE^2 = 2AE^2$.
综上, ①②③④均正确.
答案：A
2. 如图,在 $\triangle ABC$ 中,$\angle BAC = 90^{\circ}$,$AB = AC$,点 $D$,$E$ 均在边 $BC$ 上,且 $\angle DAE = 45^{\circ}$,若 $BD = 4$,$CE = 3$,则 $DE= $______
5
。答案：5
解析：
证明：将$\triangle ABD$绕点$A$顺时针旋转$90^{\circ}$得到$\triangle ACF$，连接$EF$。
$\because \angle BAC=90^{\circ}$，$AB=AC$，
$\therefore \angle B=\angle ACB=45^{\circ}$。
由旋转性质得：$CF=BD=4$，$AF=AD$，$\angle CAF=\angle BAD$，$\angle ACF=\angle B=45^{\circ}$。
$\because \angle DAE=45^{\circ}$，
$\therefore \angle BAD+\angle CAE=45^{\circ}$，
$\therefore \angle CAF+\angle CAE=45^{\circ}$，即$\angle EAF=45^{\circ}$。
在$\triangle AEF$和$\triangle AED$中，
$\left\{\begin{array}{l}AF=AD \\ \angle EAF=\angle EAD \\ AE=AE\end{array}\right.$，
$\therefore \triangle AEF \cong \triangle AED(SAS)$，
$\therefore EF=DE$。
$\because \angle ECF=\angle ACB+\angle ACF=45^{\circ}+45^{\circ}=90^{\circ}$，
$\therefore$在$Rt\triangle ECF$中，$EF^{2}=CE^{2}+CF^{2}=3^{2}+4^{2}=25$，
$\therefore EF=5$，即$DE=5$。
$5$
$\because \angle BAC=90^{\circ}$，$AB=AC$，
$\therefore \angle B=\angle ACB=45^{\circ}$。
由旋转性质得：$CF=BD=4$，$AF=AD$，$\angle CAF=\angle BAD$，$\angle ACF=\angle B=45^{\circ}$。
$\because \angle DAE=45^{\circ}$，
$\therefore \angle BAD+\angle CAE=45^{\circ}$，
$\therefore \angle CAF+\angle CAE=45^{\circ}$，即$\angle EAF=45^{\circ}$。
在$\triangle AEF$和$\triangle AED$中，
$\left\{\begin{array}{l}AF=AD \\ \angle EAF=\angle EAD \\ AE=AE\end{array}\right.$，
$\therefore \triangle AEF \cong \triangle AED(SAS)$，
$\therefore EF=DE$。
$\because \angle ECF=\angle ACB+\angle ACF=45^{\circ}+45^{\circ}=90^{\circ}$，
$\therefore$在$Rt\triangle ECF$中，$EF^{2}=CE^{2}+CF^{2}=3^{2}+4^{2}=25$，
$\therefore EF=5$，即$DE=5$。
$5$
3. 如图,在等腰直角三角形 $ABC$ 中,$AB = AC$,$D$,$E$ 是斜边 $BC$ 上两点,且 $\angle DAE = 45^{\circ}$,若 $BD = 6$,$CE = 8$,则 $\triangle ABD$ 与 $\triangle ADE$ 的面积之比为
3:5
。答案：3:5
解析：
证明：将△ABD绕点A逆时针旋转90°至△ACF，连接EF。
∵AB=AC，∠BAC=90°，
∴∠B=∠ACB=45°，旋转后AB与AC重合，∠ACF=∠B=45°，CF=BD=6，∠CAF=∠BAD。
∵∠DAE=45°，
∴∠BAD+∠CAE=45°，
∴∠CAF+∠CAE=∠EAF=45°=∠DAE。
在△ADE和△AFE中，
AD=AF，∠DAE=∠FAE，AE=AE，
∴△ADE≌△AFE(SAS)，
∴DE=EF。
∵∠ECF=∠ACB+∠ACF=45°+45°=90°，
∴△ECF是直角三角形。
∵CE=8，CF=6，
∴EF=√(CE²+CF²)=√(8²+6²)=10，
∴DE=10。
设BC=BD+DE+EC=6+10+8=24，
等腰直角三角形ABC中，BC边上的高h=BC/2=12，
S△ABC=1/2×24×12=144。
设AB=AC=x，由勾股定理x²+x²=24²，得x=12√2，
S△ABD=1/2×BD×h1，S△AEC=1/2×CE×h2，S△ADE=1/2×DE×h3，其中h1+h2+h3=h=12。
S△ABD+S△AEC+S△ADE=S△ABC=144，
1/2×6×h1 + 1/2×8×h2 + 1/2×10×h3=144，
即3h1+4h2+5h3=144。
又h1+h2+h3=12，设h3=12 - h1 - h2，代入得3h1+4h2+5(12 - h1 - h2)=144，
化简得-2h1 - h2=84，此式不成立，改用面积法另解：
设△ABD中BD边上的高为h1，△ADE中DE边上的高为h2，△AEC中EC边上的高为h3，
∵三个三角形同高（顶点A到BC的距离），即h1=h2=h3=h=12（错误，应为同顶点A到BC的距离，即三个三角形的高均为A到BC的距离，即h=12），
S△ABD=1/2×6×12=36，S△ADE=1/2×10×12=60，
∴S△ABD:S△ADE=36:60=3:5。
3:5
∵AB=AC，∠BAC=90°，
∴∠B=∠ACB=45°，旋转后AB与AC重合，∠ACF=∠B=45°，CF=BD=6，∠CAF=∠BAD。
∵∠DAE=45°，
∴∠BAD+∠CAE=45°，
∴∠CAF+∠CAE=∠EAF=45°=∠DAE。
在△ADE和△AFE中，
AD=AF，∠DAE=∠FAE，AE=AE，
∴△ADE≌△AFE(SAS)，
∴DE=EF。
∵∠ECF=∠ACB+∠ACF=45°+45°=90°，
∴△ECF是直角三角形。
∵CE=8，CF=6，
∴EF=√(CE²+CF²)=√(8²+6²)=10，
∴DE=10。
设BC=BD+DE+EC=6+10+8=24，
等腰直角三角形ABC中，BC边上的高h=BC/2=12，
S△ABC=1/2×24×12=144。
设AB=AC=x，由勾股定理x²+x²=24²，得x=12√2，
S△ABD=1/2×BD×h1，S△AEC=1/2×CE×h2，S△ADE=1/2×DE×h3，其中h1+h2+h3=h=12。
S△ABD+S△AEC+S△ADE=S△ABC=144，
1/2×6×h1 + 1/2×8×h2 + 1/2×10×h3=144，
即3h1+4h2+5h3=144。
又h1+h2+h3=12，设h3=12 - h1 - h2，代入得3h1+4h2+5(12 - h1 - h2)=144，
化简得-2h1 - h2=84，此式不成立，改用面积法另解：
设△ABD中BD边上的高为h1，△ADE中DE边上的高为h2，△AEC中EC边上的高为h3，
∵三个三角形同高（顶点A到BC的距离），即h1=h2=h3=h=12（错误，应为同顶点A到BC的距离，即三个三角形的高均为A到BC的距离，即h=12），
S△ABD=1/2×6×12=36，S△ADE=1/2×10×12=60，
∴S△ABD:S△ADE=36:60=3:5。
3:5
4. 如图,$\angle BAC = \angle DAF = 90^{\circ}$,$AB = AC$,$AD = AF$,$D$,$E$ 为 $BC$ 边上的两点,且 $\angle DAE = 45^{\circ}$,连接 $EF$,$BF$,则下列结论正确的是______。(填序号)
①$\triangle AED\cong\triangle AEF$；②$\triangle AED$ 为等腰三角形；③$BE + DC＞DE$；④$BE^{2}+DC^{2}＞DE^{2}$。
①$\triangle AED\cong\triangle AEF$；②$\triangle AED$ 为等腰三角形；③$BE + DC＞DE$；④$BE^{2}+DC^{2}＞DE^{2}$。
①③
答案：①③
解析：
证明：
∵∠BAC=∠DAF=90°，
∴∠BAC-∠BAD=∠DAF-∠BAD，即∠CAD=∠BAF。
在△ACD和△ABF中，
$\left\{\begin{array}{l} AC=AB \\ ∠CAD=∠BAF \\ AD=AF\end{array}\right.$，
∴△ACD≌△ABF(SAS)，
∴CD=BF，∠ACD=∠ABF。
∵AB=AC，∠BAC=90°，
∴∠ABC=∠ACB=45°，
∴∠ABF=45°，
∴∠EBF=∠ABC+∠ABF=90°。
∵∠DAF=90°，∠DAE=45°，
∴∠FAE=∠DAF-∠DAE=45°，
在△AED和△AEF中，
$\left\{\begin{array}{l} AD=AF \\ ∠DAE=∠FAE \\ AE=AE\end{array}\right.$，
∴△AED≌△AEF(SAS)，故①正确。
∵△AED≌△AEF，
∴DE=EF。
在Rt△BEF中，BE+BF＞EF，
∵BF=CD，EF=DE，
∴BE+CD＞DE，故③正确。
在Rt△BEF中，BE²+BF²=EF²，
∵BF=CD，EF=DE，
∴BE²+CD²=DE²，故④错误。
无法证明△AED为等腰三角形，故②错误。
结论：①③
∵∠BAC=∠DAF=90°，
∴∠BAC-∠BAD=∠DAF-∠BAD，即∠CAD=∠BAF。
在△ACD和△ABF中，
$\left\{\begin{array}{l} AC=AB \\ ∠CAD=∠BAF \\ AD=AF\end{array}\right.$，
∴△ACD≌△ABF(SAS)，
∴CD=BF，∠ACD=∠ABF。
∵AB=AC，∠BAC=90°，
∴∠ABC=∠ACB=45°，
∴∠ABF=45°，
∴∠EBF=∠ABC+∠ABF=90°。
∵∠DAF=90°，∠DAE=45°，
∴∠FAE=∠DAF-∠DAE=45°，
在△AED和△AEF中，
$\left\{\begin{array}{l} AD=AF \\ ∠DAE=∠FAE \\ AE=AE\end{array}\right.$，
∴△AED≌△AEF(SAS)，故①正确。
∵△AED≌△AEF，
∴DE=EF。
在Rt△BEF中，BE+BF＞EF，
∵BF=CD，EF=DE，
∴BE+CD＞DE，故③正确。
在Rt△BEF中，BE²+BF²=EF²，
∵BF=CD，EF=DE，
∴BE²+CD²=DE²，故④错误。
无法证明△AED为等腰三角形，故②错误。
结论：①③