10. (15 分)(2024·南京玄武区期末)中国象棋是经典国粹,备受人们喜爱。如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走。例如:图中“马”所在的位置可以直接走到点 $ A $ 或点 $ B $ 处等。若对象棋棋盘建立恰当的平面直角坐标系,可以便于研究和解决问题。
(1)如图,若“帅”所在点的坐标为 $ (1,-1) $,“马”所在的点的坐标为 $ (-2,-1) $,则“相”所在点的坐标为
(2)如图,若 $ C $ 点的坐标为 $ (2,2) $,$ D $ 点的坐标为 $ (4,0) $,按“马”走的规则,图中“马”由所在的位置走一步可以直接到的点的坐标为
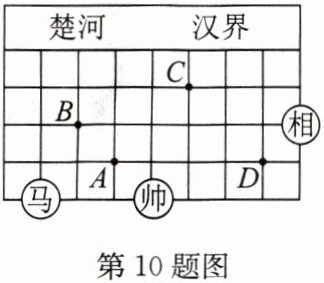
(1)如图,若“帅”所在点的坐标为 $ (1,-1) $,“马”所在的点的坐标为 $ (-2,-1) $,则“相”所在点的坐标为
(5,1)
;(2)如图,若 $ C $ 点的坐标为 $ (2,2) $,$ D $ 点的坐标为 $ (4,0) $,按“马”走的规则,图中“马”由所在的位置走一步可以直接到的点的坐标为
(0,0),(-1,1),(-3,1)
。
答案:
(1)(5,1)
(2)(0,0),(-1,1),(-3,1)
(1)(5,1)
(2)(0,0),(-1,1),(-3,1)
11. (16 分)先阅读材料,再回答相应的问题。
在平面直角坐标系中,有 $ P_1(x_1,y_1) $,$ P_2(x_2,y_2) $ 两点,则 $ P_1 $,$ P_2 $ 两点间的距离可表示为 $ P_1P_2 = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $。
(1)已知点 $ A(-2,1) $,$ B(1,5) $,求 $ A $,$ B $ 两点间的距离;
(2)已知点 $ A $,$ B $ 在平行于 $ x $ 轴的直线上,点 $ A $ 的横坐标为 -5,点 $ B $ 的横坐标为 3,试求 $ A $,$ B $ 两点间的距离;
(3)若一个三角形各顶点的坐标为 $ A(-2,0) $,$ B(2,0) $,$ C(0,2\sqrt{3}) $,试判断 $ \triangle ABC $ 的形状。
在平面直角坐标系中,有 $ P_1(x_1,y_1) $,$ P_2(x_2,y_2) $ 两点,则 $ P_1 $,$ P_2 $ 两点间的距离可表示为 $ P_1P_2 = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $。
(1)已知点 $ A(-2,1) $,$ B(1,5) $,求 $ A $,$ B $ 两点间的距离;
(2)已知点 $ A $,$ B $ 在平行于 $ x $ 轴的直线上,点 $ A $ 的横坐标为 -5,点 $ B $ 的横坐标为 3,试求 $ A $,$ B $ 两点间的距离;
(3)若一个三角形各顶点的坐标为 $ A(-2,0) $,$ B(2,0) $,$ C(0,2\sqrt{3}) $,试判断 $ \triangle ABC $ 的形状。
答案:解:
(1)AB=√[(1+2)²+(5-1)²]=√[9+16]=5.
(2)由题意可设A(-5,y₀),B(3,y₀),则AB=√[(3+5)²+(y₀-y₀)²]=√[64]=8.
(3)
∵AB=√[(2+2)²+(0-0)²]=4,AC=√[(0+2)²+(2√3-0)²]=4,BC=√[(0-2)²+(2√3-0)²]=4,
∴AB=AC=BC,
∴△ABC是等边三角形.
(1)AB=√[(1+2)²+(5-1)²]=√[9+16]=5.
(2)由题意可设A(-5,y₀),B(3,y₀),则AB=√[(3+5)²+(y₀-y₀)²]=√[64]=8.
(3)
∵AB=√[(2+2)²+(0-0)²]=4,AC=√[(0+2)²+(2√3-0)²]=4,BC=√[(0-2)²+(2√3-0)²]=4,
∴AB=AC=BC,
∴△ABC是等边三角形.
12. (20 分)已知点 $ P(2m + 4,m - 1) $。试分别根据下列条件,求出点 $ P $ 的坐标。
(1)点 $ P $ 在 $ y $ 轴上;
(2)到 $ x $ 轴的距离为 2;
(3)点 $ P $ 在第四象限内,且点 $ P $ 到两坐标轴的距离之和为 4;
(4)点 $ P $ 在过点 $ A(2,-3) $ 且与 $ x $ 轴平行的直线上。
(1)点 $ P $ 在 $ y $ 轴上;
(2)到 $ x $ 轴的距离为 2;
(3)点 $ P $ 在第四象限内,且点 $ P $ 到两坐标轴的距离之和为 4;
(4)点 $ P $ 在过点 $ A(2,-3) $ 且与 $ x $ 轴平行的直线上。
答案:解:
(1)由题意,得2m+4=0,
∴m=-2,
∴点P的坐标为(0,-3).
(2)由题意,得|m-1|=2,
∴m=3或m=-1,
∴点P的坐标为(10,2)或(2,-2).
(3)由题意,得2m+4+[-(m-1)]=4,
∴m=-1,
∴点P的坐标为(2,-2).
(4)令m-1=-3,解得m=-2,
∴点P的坐标为(0,-3).
(1)由题意,得2m+4=0,
∴m=-2,
∴点P的坐标为(0,-3).
(2)由题意,得|m-1|=2,
∴m=3或m=-1,
∴点P的坐标为(10,2)或(2,-2).
(3)由题意,得2m+4+[-(m-1)]=4,
∴m=-1,
∴点P的坐标为(2,-2).
(4)令m-1=-3,解得m=-2,
∴点P的坐标为(0,-3).