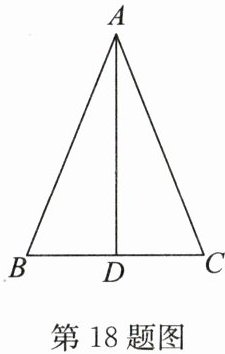
18. (6分)如图,AD是△ABC的中线,AD= 24,AB= 26,BC= 20. 求AC的长.

答案:解:
∵AD是△ABC的中线,BC=20,
∴BD=$\frac{1}{2}$BC=10.又
∵AD=24,AB=26,
∴BD²+AD²=AB²,
∴AD⊥BC,
∴AD垂直平分BC,
∴AC=AB=26.
∵AD是△ABC的中线,BC=20,
∴BD=$\frac{1}{2}$BC=10.又
∵AD=24,AB=26,
∴BD²+AD²=AB²,
∴AD⊥BC,
∴AD垂直平分BC,
∴AC=AB=26.
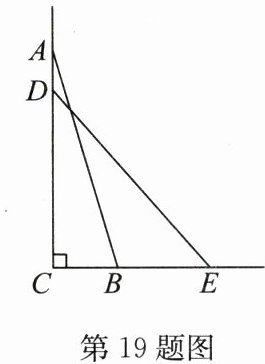
19. (8分)如图,一架云梯AB长25 m,斜靠在一面墙上,梯子靠墙的一端A距地面24 m.
(1)这个梯子底端B离墙多少米?
(2)如果梯子的顶端下滑的距离AD= 4 m,求梯子的底部B在水平方向滑动的距离BE的长.
(1)这个梯子底端B离墙多少米?
(2)如果梯子的顶端下滑的距离AD= 4 m,求梯子的底部B在水平方向滑动的距离BE的长.

答案:解:
(1)在Rt△ABC中,AB=25m,AC=24m,由勾股定理,得$BC^{2}=AB^{2}-AC^{2}=25^{2}-24^{2}=49$,解得BC=7,即这个梯子底端B离墙7m.
(2)在Rt△DCE中,DE=25m,DC=24−4=20(m).由勾股定理,得$CE^{2}=DE^{2}-DC^{2}=25^{2}-20^{2}=225$,解得CE=15.
∴BE=CE−BC=15−7=8(m).
∴梯子的底部B在水平方向滑动的距离BE的长为8m.
(1)在Rt△ABC中,AB=25m,AC=24m,由勾股定理,得$BC^{2}=AB^{2}-AC^{2}=25^{2}-24^{2}=49$,解得BC=7,即这个梯子底端B离墙7m.
(2)在Rt△DCE中,DE=25m,DC=24−4=20(m).由勾股定理,得$CE^{2}=DE^{2}-DC^{2}=25^{2}-20^{2}=225$,解得CE=15.
∴BE=CE−BC=15−7=8(m).
∴梯子的底部B在水平方向滑动的距离BE的长为8m.
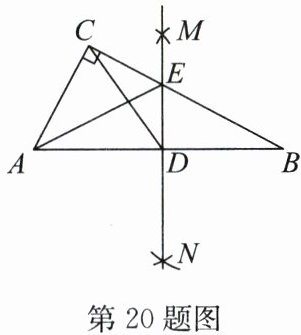
20. (8分)(2024·长沙)如图,在Rt△ABC中,∠ACB= 90°,AB= 2$\sqrt{5}$,AC= 2,分别以点A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧分别交于点M,N,作直线MN分别交AB,BC于点D,E,连接CD,AE.
求:(1)CD的长;(2)△ACE的周长.
求:(1)CD的长;(2)△ACE的周长.

答案:解:
(1)由作图过程可知,直线MN为线段AB的垂直平分线,
∴D为AB的中点.又
∵∠ACB=90°,
∴CD=$\frac{1}{2}$AB=$\sqrt{5}$.
(2)在Rt△ABC中,由勾股定理,得$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{(2\sqrt{5})^{2}-2^{2}}=4$.
∵直线MN为线段AB的垂直平分线,
∴EA=EB.
∴△ACE的周长为AC+CE+EA=AC+CE+EB=AC+BC=2+4=6.
(1)由作图过程可知,直线MN为线段AB的垂直平分线,
∴D为AB的中点.又
∵∠ACB=90°,
∴CD=$\frac{1}{2}$AB=$\sqrt{5}$.
(2)在Rt△ABC中,由勾股定理,得$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{(2\sqrt{5})^{2}-2^{2}}=4$.
∵直线MN为线段AB的垂直平分线,
∴EA=EB.
∴△ACE的周长为AC+CE+EA=AC+CE+EB=AC+BC=2+4=6.