23. (8分)如图,已知直线$ l _ { 1 } : y _ { 1 } = - \frac { 1 } { 2 } x + 1 $与x轴交于点A,与直线$ l _ { 2 } : y _ { 2 } = - \frac { 3 } { 2 } x $交于点B.
(1)求$ \triangle A O B $的面积;
(2)求当$ y _ { 1 } > y _ { 2 } $时,x的取值范围.

(1)求$ \triangle A O B $的面积;
(2)求当$ y _ { 1 } > y _ { 2 } $时,x的取值范围.

答案:解:
(1)在y=−$\frac{1}{2}$x+1中,令y=0,得x=2,
∴A(2,0),
∴OA=2.联立$\begin{cases}y = -\frac{1}{2}x + 1 \\ y = -\frac{3}{2}x \end{cases}$,解得$\begin{cases}x = -1 \\ y = \frac{3}{2} \end{cases}$,
∴B(−1,$\frac{3}{2}$).
∴S$_{\triangle AOB}$=$\frac{1}{2}$OA·|y$_B$|=$\frac{1}{2}$×2×$\frac{3}{2}$=$\frac{3}{2}$.
(2)由图象可知当y₁>y₂时,x的取值范围是x>−1.
(1)在y=−$\frac{1}{2}$x+1中,令y=0,得x=2,
∴A(2,0),
∴OA=2.联立$\begin{cases}y = -\frac{1}{2}x + 1 \\ y = -\frac{3}{2}x \end{cases}$,解得$\begin{cases}x = -1 \\ y = \frac{3}{2} \end{cases}$,
∴B(−1,$\frac{3}{2}$).
∴S$_{\triangle AOB}$=$\frac{1}{2}$OA·|y$_B$|=$\frac{1}{2}$×2×$\frac{3}{2}$=$\frac{3}{2}$.
(2)由图象可知当y₁>y₂时,x的取值范围是x>−1.
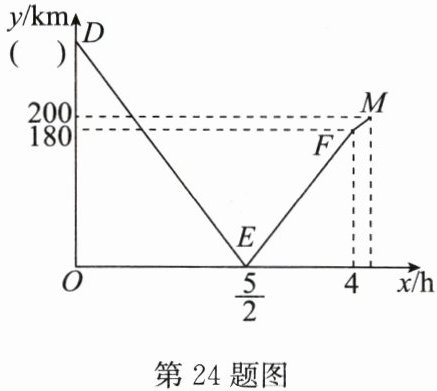
24. (12分)(2024·牡丹江)一条公路上依次有A,B,C三地,甲车从A地出发,沿公路经B地到C地,乙车从C地出发,沿公路驶向B地. 甲、乙两车同时出发,匀速行驶,乙车比甲车早$ \frac { 2 } { 7 } \mathrm { h } $到达目的地. 甲、乙两车之间的路程$ y \mathrm { km } 与两车行驶时间 x \mathrm { h } $的函数关系如图所示,请结合图象信息,解答下列问题:
(1)甲车的行驶速度是______km/h,并在图中括号内填上正确的数;
(2)求图中线段EF所在直线的函数表达式(不要求写出自变量的取值范围);
(3)请直接写出甲、乙两车出发多少小时,乙车距B地的路程是甲车距B地路程的3倍.
(1)甲车的行驶速度是______km/h,并在图中括号内填上正确的数;
(2)求图中线段EF所在直线的函数表达式(不要求写出自变量的取值范围);
(3)请直接写出甲、乙两车出发多少小时,乙车距B地的路程是甲车距B地路程的3倍.

答案:
(1)70 点拨:由题图可知,甲车$\frac{2}{7}$h行驶的路程为(200−180)km,
∴甲车的行驶速度是(200−180)÷$\frac{2}{7}$=70(km/h),70×(4+$\frac{2}{7}$)=300(km).如答图,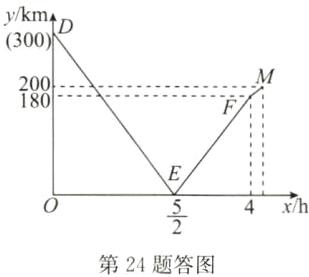
(2)解:由题图可知点E,F的坐标分别为($\frac{5}{2}$,0),(4,180).设线段EF所在直线的函数表达式为y=kx+b,则$\begin{cases}\frac{5}{2}k + b = 0 \\ 4k + b = 180 \end{cases}$,解得$\begin{cases}k = 120 \\ b = -300 \end{cases}$,
∴线段EF所在直线的函数表达式为y=120x−300.
(3)解:由题意知,A,C两地间的距离为(4+$\frac{2}{7}$)×70=300(km),乙车的行驶速度为300÷$\frac{5}{2}$−70=50(km/h),C,B两地间的距离为50×4=200(km),A,B两地间的距离为300−200=100(km).设两车出发x h,乙车距B地的路程是甲车距B地路程的3倍.分两种情况:当甲到达B地前,200−50x=3(100−70x),解得x=$\frac{5}{8}$;当甲到达B地后,200−50x=3(70x−100),解得x=$\frac{25}{13}$.综上可知,甲、乙两车出发$\frac{5}{8}$h或$\frac{25}{13}$h时,乙车距B地的路程是甲车距B地路程的3倍.
(1)70 点拨:由题图可知,甲车$\frac{2}{7}$h行驶的路程为(200−180)km,
∴甲车的行驶速度是(200−180)÷$\frac{2}{7}$=70(km/h),70×(4+$\frac{2}{7}$)=300(km).如答图,

(2)解:由题图可知点E,F的坐标分别为($\frac{5}{2}$,0),(4,180).设线段EF所在直线的函数表达式为y=kx+b,则$\begin{cases}\frac{5}{2}k + b = 0 \\ 4k + b = 180 \end{cases}$,解得$\begin{cases}k = 120 \\ b = -300 \end{cases}$,
∴线段EF所在直线的函数表达式为y=120x−300.
(3)解:由题意知,A,C两地间的距离为(4+$\frac{2}{7}$)×70=300(km),乙车的行驶速度为300÷$\frac{5}{2}$−70=50(km/h),C,B两地间的距离为50×4=200(km),A,B两地间的距离为300−200=100(km).设两车出发x h,乙车距B地的路程是甲车距B地路程的3倍.分两种情况:当甲到达B地前,200−50x=3(100−70x),解得x=$\frac{5}{8}$;当甲到达B地后,200−50x=3(70x−100),解得x=$\frac{25}{13}$.综上可知,甲、乙两车出发$\frac{5}{8}$h或$\frac{25}{13}$h时,乙车距B地的路程是甲车距B地路程的3倍.