1. (2024·张家港期末)已知直线 $ MN $ 平行于 $ x $ 轴,若点 $ M $ 的坐标为 $ (-1,3) $,且点 $ N $ 到 $ y $ 轴的距离等于 $ 4 $,则点 $ N $ 的坐标是 (
A.$ (-1,4) $
B.$ (4,3) $
C.$ (-1,4) 或 (1,-4) $
D.$ (4,3) 或 (-4,3) $
D
)A.$ (-1,4) $
B.$ (4,3) $
C.$ (-1,4) 或 (1,-4) $
D.$ (4,3) 或 (-4,3) $
答案:D
解析:
∵直线$MN$平行于$x$轴,点$M$的坐标为$(-1,3)$,
∴点$N$的纵坐标与点$M$的纵坐标相同,为$3$。
∵点$N$到$y$轴的距离等于$4$,
∴点$N$的横坐标为$4$或$-4$。
∴点$N$的坐标是$(4,3)$或$(-4,3)$。
D
2. 将直线 $ y = x - 1 $ 向上平移 $ 2 $ 个单位长度后得到直线 $ y = kx + b $,则下列关于直线 $ y = kx + b $ 的说法正确的是 (
A.经过第一、二、四象限
B.与 $ x $ 轴交于点$ (1,0) $
C.与 $ y $ 轴交于点$ (0,1) $
D.$ y $ 随 $ x $ 的增大而减小
C
)A.经过第一、二、四象限
B.与 $ x $ 轴交于点$ (1,0) $
C.与 $ y $ 轴交于点$ (0,1) $
D.$ y $ 随 $ x $ 的增大而减小
答案:C
解析:
将直线$y = x - 1$向上平移$2$个单位长度,根据平移规律“上加下减”,得到的直线解析式为$y = x - 1 + 2 = x + 1$,即$k = 1$,$b = 1$。
对于直线$y = x + 1$:
因为$k = 1>0$,$b = 1>0$,所以直线经过第一、二、三象限,A选项错误;
令$y = 0$,则$x + 1 = 0$,解得$x=-1$,所以与$x$轴交于点$(-1,0)$,B选项错误;
令$x = 0$,则$y = 0 + 1 = 1$,所以与$y$轴交于点$(0,1)$,C选项正确;
因为$k = 1>0$,所以$y$随$x$的增大而增大,D选项错误。
C
对于直线$y = x + 1$:
因为$k = 1>0$,$b = 1>0$,所以直线经过第一、二、三象限,A选项错误;
令$y = 0$,则$x + 1 = 0$,解得$x=-1$,所以与$x$轴交于点$(-1,0)$,B选项错误;
令$x = 0$,则$y = 0 + 1 = 1$,所以与$y$轴交于点$(0,1)$,C选项正确;
因为$k = 1>0$,所以$y$随$x$的增大而增大,D选项错误。
C
3. 如图,用直尺和圆规作 $ \angle BAD $ 的平分线 $ AG $,过点 $ B $ 作 $ BC // AD $,交 $ AG $ 于点 $ E $,$ BF = 6 $,$ AB = 5 $,则 $ AE $ 的长为 (

A.$ 10 $
B.$ 8 $
C.$ 6 $
D.$ 4 $
B
)
A.$ 10 $
B.$ 8 $
C.$ 6 $
D.$ 4 $
答案:B
解析:
证明:
∵AG平分∠BAD,
∴∠BAE=∠DAE.
∵BC//AD,
∴∠AEB=∠DAE.
∴∠BAE=∠AEB,
∴AB=BE=5.
由作图知AG垂直平分BF,设垂足为H,则BH=HF=3,∠AHB=90°.
在Rt△ABH中,
$AH=\sqrt{AB^2-BH^2}=\sqrt{5^2-3^2}=4$.
设AE=x,则EH=AE-AH=x-4.
在Rt△BHE中,
$BH^2+EH^2=BE^2$,
即$3^2+(x-4)^2=5^2$,
解得x=8(x=0舍去).
∴AE=8.
B
∵AG平分∠BAD,
∴∠BAE=∠DAE.
∵BC//AD,
∴∠AEB=∠DAE.
∴∠BAE=∠AEB,
∴AB=BE=5.
由作图知AG垂直平分BF,设垂足为H,则BH=HF=3,∠AHB=90°.
在Rt△ABH中,
$AH=\sqrt{AB^2-BH^2}=\sqrt{5^2-3^2}=4$.
设AE=x,则EH=AE-AH=x-4.
在Rt△BHE中,
$BH^2+EH^2=BE^2$,
即$3^2+(x-4)^2=5^2$,
解得x=8(x=0舍去).
∴AE=8.
B
4. 如图,在锐角三角形 $ ABC $ 中,$ AB = 2 $,$ \angle BAC = 45^{\circ} $,$ \angle BAC $ 的平分线交 $ BC $ 于点 $ D $. $ M $,$ N $ 分别是 $ AD $ 和 $ AB $ 上的动点,则 $ BM + MN $ 的最小值是 (

A.$ 2 $
B.$ 3 $
C.$ \sqrt{2} $
D.$ \sqrt{3} $
C
)
A.$ 2 $
B.$ 3 $
C.$ \sqrt{2} $
D.$ \sqrt{3} $
答案:C
解析:
证明:在AC上截取AE=AN,连接ME。
∵AD平分∠BAC,
∴∠EAM=∠NAM。
在△AME和△AMN中,
$\left\{\begin{array}{l} AE=AN \\ \angle EAM=\angle NAM \\ AM=AM \end{array}\right.$
∴△AME≌△AMN(SAS),
∴ME=MN。
∴BM+MN=BM+ME。
当B,M,E三点共线且BE⊥AC时,BM+ME最小,即BM+MN最小。
∵AB=2,∠BAC=45°,BE⊥AC,
∴BE=AB·sin45°=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$。
故BM+MN的最小值为$\sqrt{2}$。
C
∵AD平分∠BAC,
∴∠EAM=∠NAM。
在△AME和△AMN中,
$\left\{\begin{array}{l} AE=AN \\ \angle EAM=\angle NAM \\ AM=AM \end{array}\right.$
∴△AME≌△AMN(SAS),
∴ME=MN。
∴BM+MN=BM+ME。
当B,M,E三点共线且BE⊥AC时,BM+ME最小,即BM+MN最小。
∵AB=2,∠BAC=45°,BE⊥AC,
∴BE=AB·sin45°=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$。
故BM+MN的最小值为$\sqrt{2}$。
C
5. 比较大小:$ \frac{\sqrt{5}}{2} $
>
$ 1 $.(填“$ > $”“$ < $”或“$ = $”)答案:>
解析:
$\because \sqrt{5} \approx 2.236$,$\therefore \frac{\sqrt{5}}{2} \approx 1.118$,$1.118>1$,$\therefore \frac{\sqrt{5}}{2}>1$
>
>
6. 已知点 $ A(a - 1,2) $ 与点 $ A'(2,b + 1) $ 关于 $ y $ 轴对称,则 $ a + b $ 的值为
0
.答案:0
解析:
因为点 $ A(a - 1,2) $ 与点 $ A'(2,b + 1) $ 关于 $ y $ 轴对称,所以横坐标互为相反数,纵坐标相等。
则 $ a - 1 = -2 $,解得 $ a = -1 $;
$ b + 1 = 2 $,解得 $ b = 1 $。
所以 $ a + b = -1 + 1 = 0 $。
0
则 $ a - 1 = -2 $,解得 $ a = -1 $;
$ b + 1 = 2 $,解得 $ b = 1 $。
所以 $ a + b = -1 + 1 = 0 $。
0
7. 一次函数 $ y = ax + b $ 与正比例函数 $ y = kx $ 在同一平面直角坐标系的图象如图所示,则关于 $ x $ 的不等式 $ ax + b \geqslant kx $ 的解集为

x≥-1
.
答案:x≥-1
解析:
解:由图可知,一次函数 $ y = ax + b $ 与正比例函数 $ y = kx $ 的交点横坐标为 $ x = -1 $。
当 $ x \geq -1 $ 时,一次函数 $ y = ax + b $ 的图象在正比例函数 $ y = kx $ 的图象上方或重合,即 $ ax + b \geq kx $。
故不等式 $ ax + b \geq kx $ 的解集为 $ x \geq -1 $。
$ x \geq -1 $
当 $ x \geq -1 $ 时,一次函数 $ y = ax + b $ 的图象在正比例函数 $ y = kx $ 的图象上方或重合,即 $ ax + b \geq kx $。
故不等式 $ ax + b \geq kx $ 的解集为 $ x \geq -1 $。
$ x \geq -1 $
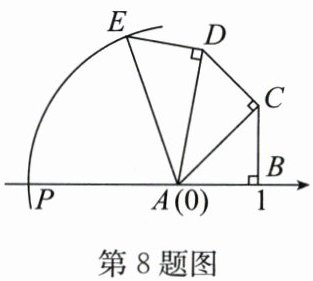
8. 如图,$ AB = BC = CD = DE $,$ \angle CBA = \angle DCA = \angle EDA = 90^{\circ} $,以点 $ A $ 为圆心,$ AE $ 长为半径画弧与数轴交于点 $ P $,点 $ A $,$ B $ 表示的数分别为 $ 0 $,$ 1 $,则点 $ P $ 表示的数为
-2
.
答案:-2
解析:
解:
∵点$A$表示的数为$0$,点$B$表示的数为$1$,
∴$AB = 1$。
∵$AB = BC = CD = DE$,
∴$BC = CD = DE = 1$。
在$Rt\triangle ABC$中,$AC^2 = AB^2 + BC^2 = 1^2 + 1^2 = 2$,
∴$AC = \sqrt{2}$。
在$Rt\triangle ACD$中,$AD^2 = AC^2 + CD^2 = (\sqrt{2})^2 + 1^2 = 3$,
∴$AD = \sqrt{3}$。
在$Rt\triangle ADE$中,$AE^2 = AD^2 + DE^2 = (\sqrt{3})^2 + 1^2 = 4$,
∴$AE = 2$。
∵以点$A$为圆心,$AE$长为半径画弧与数轴交于点$P$,
∴$AP = AE = 2$。
∵点$P$在点$A$左侧,
∴点$P$表示的数为$-2$。
$-2$
∵点$A$表示的数为$0$,点$B$表示的数为$1$,
∴$AB = 1$。
∵$AB = BC = CD = DE$,
∴$BC = CD = DE = 1$。
在$Rt\triangle ABC$中,$AC^2 = AB^2 + BC^2 = 1^2 + 1^2 = 2$,
∴$AC = \sqrt{2}$。
在$Rt\triangle ACD$中,$AD^2 = AC^2 + CD^2 = (\sqrt{2})^2 + 1^2 = 3$,
∴$AD = \sqrt{3}$。
在$Rt\triangle ADE$中,$AE^2 = AD^2 + DE^2 = (\sqrt{3})^2 + 1^2 = 4$,
∴$AE = 2$。
∵以点$A$为圆心,$AE$长为半径画弧与数轴交于点$P$,
∴$AP = AE = 2$。
∵点$P$在点$A$左侧,
∴点$P$表示的数为$-2$。
$-2$