1. 如图,点 $ E $,$ F $ 在 $ AC $ 上,$ AD = BC $,$ DF = BE $,要使 $ \triangle ADF \cong \triangle CBE $,还可以添加一个条件是(

A.$ AD // BC $
B.$ DF // BE $
C.$ \angle A = \angle C $
D.$ \angle D = \angle B $
D
)
A.$ AD // BC $
B.$ DF // BE $
C.$ \angle A = \angle C $
D.$ \angle D = \angle B $
答案:D
解析:
要使$\triangle ADF \cong \triangle CBE$,已知$AD = BC$,$DF = BE$。
选项A:$AD // BC$,可推出$\angle A = \angle C$,但“边边角”不能判定全等。
选项B:$DF // BE$,可推出$\angle DFA = \angle BEC$,但“边边角”不能判定全等。
选项C:$\angle A = \angle C$,“边边角”不能判定全等。
选项D:$\angle D = \angle B$,结合$AD = BC$,$DF = BE$,符合“边角边”(SAS)判定定理,可证$\triangle ADF \cong \triangle CBE$。
D
选项A:$AD // BC$,可推出$\angle A = \angle C$,但“边边角”不能判定全等。
选项B:$DF // BE$,可推出$\angle DFA = \angle BEC$,但“边边角”不能判定全等。
选项C:$\angle A = \angle C$,“边边角”不能判定全等。
选项D:$\angle D = \angle B$,结合$AD = BC$,$DF = BE$,符合“边角边”(SAS)判定定理,可证$\triangle ADF \cong \triangle CBE$。
D
2. 一次函数 $ y = kx - 1 $ 的图象经过点 $ P $,且 $ y $ 的值随 $ x $ 值的增大而增大,则点 $ P $ 的坐标可以为(
A.$ (5,-1) $
B.$ (1,-3) $
C.$ (-5,1) $
D.$ (5,3) $
D
)A.$ (5,-1) $
B.$ (1,-3) $
C.$ (-5,1) $
D.$ (5,3) $
答案:D
解析:
∵一次函数$y = kx - 1$的$y$值随$x$值的增大而增大,
∴$k>0$。
对于选项A:将$(5,-1)$代入$y = kx - 1$,得$-1 = 5k - 1$,解得$k = 0$,不符合$k>0$。
对于选项B:将$(1,-3)$代入$y = kx - 1$,得$-3 = k - 1$,解得$k=-2$,不符合$k>0$。
对于选项C:将$(-5,1)$代入$y = kx - 1$,得$1=-5k - 1$,解得$k=-\frac{2}{5}$,不符合$k>0$。
对于选项D:将$(5,3)$代入$y = kx - 1$,得$3 = 5k - 1$,解得$k=\frac{4}{5}$,符合$k>0$。
D
3. 面积为 $ 7 \, m^2 $ 的正方形的边长为 $ \sqrt{7} \, m $,估算 $ \sqrt{7} $ 的大小为(
A.1 和 2 之间
B.2 和 3 之间
C.3 和 4 之间
D.4 和 5 之间
B
)A.1 和 2 之间
B.2 和 3 之间
C.3 和 4 之间
D.4 和 5 之间
答案:B
解析:
因为$2^2 = 4$,$3^2 = 9$,且$4 < 7 < 9$,所以$\sqrt{4} < \sqrt{7} < \sqrt{9}$,即$2 < \sqrt{7} < 3$。
B
B
4. 如图,在 $ Rt \triangle ABC $ 中,$ \angle CAB = 90^{\circ} $,$ \triangle ABD $ 是等腰三角形,$ AB = BD = 4 $,$ CB \perp BD $,交 $ AD $ 于点 $ E $,若 $ BE = 1 $,则 $ AC = $(

A.7
B.7.5
C.8
D.8.5
B
)
A.7
B.7.5
C.8
D.8.5
答案:B
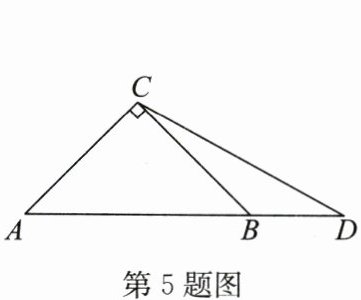
5. (2024·安徽)如图,在 $ Rt \triangle ABC $ 中,$ AC = BC = 2 $,点 $ D $ 在 $ AB $ 的延长线上,且 $ CD = AB $,则 $ BD $ 的长是(
A.$ \sqrt{10} - \sqrt{2} $
B.$ \sqrt{6} - \sqrt{2} $
C.$ 2\sqrt{2} - 2 $
D.$ 2\sqrt{2} - \sqrt{6} $
B
)
A.$ \sqrt{10} - \sqrt{2} $
B.$ \sqrt{6} - \sqrt{2} $
C.$ 2\sqrt{2} - 2 $
D.$ 2\sqrt{2} - \sqrt{6} $
答案:B
解析:
解:在$Rt\triangle ABC$中,$AC=BC=2$,$\angle ACB=90°$,
$\therefore AB=\sqrt{AC^2+BC^2}=\sqrt{2^2+2^2}=2\sqrt{2}$,
$\angle CAB=\angle CBA=45°$,
$\therefore \angle CBD=180° - 45°=135°$,
设$BD=x$,则$AD=AB+BD=2\sqrt{2}+x$,
在$\triangle BCD$中,由余弦定理得:
$CD^2=BC^2+BD^2 - 2\cdot BC\cdot BD\cdot \cos\angle CBD$,
$\because CD=AB=2\sqrt{2}$,
$\therefore (2\sqrt{2})^2=2^2 + x^2 - 2×2× x×\cos135°$,
即$8=4 + x^2 - 4x×(-\frac{\sqrt{2}}{2})$,
整理得$x^2 + 2\sqrt{2}x - 4=0$,
解得$x=\frac{-2\sqrt{2}\pm\sqrt{(2\sqrt{2})^2 + 16}}{2}=\frac{-2\sqrt{2}\pm\sqrt{8 + 16}}{2}=\frac{-2\sqrt{2}\pm\sqrt{24}}{2}=\frac{-2\sqrt{2}\pm2\sqrt{6}}{2}=-\sqrt{2}\pm\sqrt{6}$,
$\because x>0$,$\therefore x=\sqrt{6}-\sqrt{2}$,即$BD=\sqrt{6}-\sqrt{2}$。
答案:B
$\therefore AB=\sqrt{AC^2+BC^2}=\sqrt{2^2+2^2}=2\sqrt{2}$,
$\angle CAB=\angle CBA=45°$,
$\therefore \angle CBD=180° - 45°=135°$,
设$BD=x$,则$AD=AB+BD=2\sqrt{2}+x$,
在$\triangle BCD$中,由余弦定理得:
$CD^2=BC^2+BD^2 - 2\cdot BC\cdot BD\cdot \cos\angle CBD$,
$\because CD=AB=2\sqrt{2}$,
$\therefore (2\sqrt{2})^2=2^2 + x^2 - 2×2× x×\cos135°$,
即$8=4 + x^2 - 4x×(-\frac{\sqrt{2}}{2})$,
整理得$x^2 + 2\sqrt{2}x - 4=0$,
解得$x=\frac{-2\sqrt{2}\pm\sqrt{(2\sqrt{2})^2 + 16}}{2}=\frac{-2\sqrt{2}\pm\sqrt{8 + 16}}{2}=\frac{-2\sqrt{2}\pm\sqrt{24}}{2}=\frac{-2\sqrt{2}\pm2\sqrt{6}}{2}=-\sqrt{2}\pm\sqrt{6}$,
$\because x>0$,$\therefore x=\sqrt{6}-\sqrt{2}$,即$BD=\sqrt{6}-\sqrt{2}$。
答案:B
6. (2024·宿豫期末)计算:$ 2 × (-3) + \sqrt{16} - \sqrt[3]{8} + | - 5 | = $
1
.答案:1
解析:
$2×(-3)+\sqrt{16}-\sqrt[3]{8}+\vert-5\vert$
$=-6 + 4 - 2 + 5$
$=1$
$=-6 + 4 - 2 + 5$
$=1$
7. (2024·甘孜州)如图,在一个平面区域内,一台雷达探测器测得在点 $ A $,$ B $,$ C $ 处有目标出现.按某种规则,点 $ A $,$ B $ 的位置可以分别表示为 $ (1,90^{\circ}) $,$ (2,240^{\circ}) $,则点 $ C $ 的位置可以表示为______

$(3,30^{\circ })$
.
答案:$(3,30^{\circ })$
8. 如图,点 $ D $ 在 $ BC $ 边上,$ DE \perp AB $ 于点 $ E $,$ DF \perp BC $ 交 $ AC $ 边于点 $ F $,$ BD = CF $,$ BE = CD $.若 $ \angle AFD = 135^{\circ} $,则 $ \angle EDF = $

$45^{\circ }$
.
答案:$45^{\circ }$
解析:
证明:
∵ $DE \perp AB$,$DF \perp BC$,
∴ $\angle BED = \angle CDF = 90°$。
在 $Rt\triangle BED$ 和 $Rt\triangle CDF$ 中,
$\begin{cases} BD = CF \\ BE = CD \end{cases}$,
∴ $Rt\triangle BED \cong Rt\triangle CDF$(HL),
∴ $\angle BDE = \angle CFD$。
∵ $\angle AFD = 135°$,
∴ $\angle CFD = 180° - \angle AFD = 45°$,
∴ $\angle BDE = 45°$。
∵ $\angle EDF + \angle BDE = 90°$,
∴ $\angle EDF = 90° - 45° = 45°$。
$45°$
∵ $DE \perp AB$,$DF \perp BC$,
∴ $\angle BED = \angle CDF = 90°$。
在 $Rt\triangle BED$ 和 $Rt\triangle CDF$ 中,
$\begin{cases} BD = CF \\ BE = CD \end{cases}$,
∴ $Rt\triangle BED \cong Rt\triangle CDF$(HL),
∴ $\angle BDE = \angle CFD$。
∵ $\angle AFD = 135°$,
∴ $\angle CFD = 180° - \angle AFD = 45°$,
∴ $\angle BDE = 45°$。
∵ $\angle EDF + \angle BDE = 90°$,
∴ $\angle EDF = 90° - 45° = 45°$。
$45°$
9. 如图,在平面直角坐标系中,点 $ A $ 的坐标为 $ (0,1) $,点 $ B(m,2 - m) $ 与点 $ C $ 分别是直线 $ l $ 及 $ x $ 轴上的动点,则 $ \triangle ABC $ 周长的最小值为

$\sqrt {10}$
.
答案:$\sqrt {10}$
解析:
解:作点 $ A(0,1) $ 关于直线 $ y = -x + 2 $ 的对称点 $ A'(1,2) $,关于 $ x $ 轴的对称点 $ A''(0,-1) $。连接 $ A'A'' $,与直线 $ l $ 交于点 $ B $,与 $ x $ 轴交于点 $ C $。此时 $ \triangle ABC $ 周长最小,最小值为 $ A'A'' $ 的长。
$ A'A'' = \sqrt{(1 - 0)^2 + (2 - (-1))^2} = \sqrt{1 + 9} = \sqrt{10} $
$\sqrt{10}$
$ A'A'' = \sqrt{(1 - 0)^2 + (2 - (-1))^2} = \sqrt{1 + 9} = \sqrt{10} $
$\sqrt{10}$