1. 如图,已知△ABC是边长为9的等边三角形,D为AC边的中点,∠EDF= 120°,DE交线段AB于点E,DF交BC的延长线于点F。若AE= 2BE,则CF的长为( )

A.1
B.1.5
C.2
D.2.5

A.1
B.1.5
C.2
D.2.5
答案:
B 点拨:如答图,过点D作DG//BC,交AB于点G.
∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°.
∵D为AC边的中点,
∴AD=DC.
∵DG//BC,
∴∠AGD=∠B=60°,
∴∠AGD=∠A=60°,
∴△AGD是等边三角形,
∴DG=AD=CD,∠ADG=60°.
∴∠GDC=120°=∠EDF,
∴∠GDE=∠CDF.
又
∵∠DGE=∠DCF=120°,
∴△DGE≌△DCF(ASA),
∴CF=GE.
∵AB=9,AE=2BE,
∴AE=6.
又
∵AG=AD=1/2AB=4.5,
∴EG=AE−AG=1.5,
∴CF=1.5.故选B

B 点拨:如答图,过点D作DG//BC,交AB于点G.
∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°.
∵D为AC边的中点,
∴AD=DC.
∵DG//BC,
∴∠AGD=∠B=60°,
∴∠AGD=∠A=60°,
∴△AGD是等边三角形,
∴DG=AD=CD,∠ADG=60°.
∴∠GDC=120°=∠EDF,
∴∠GDE=∠CDF.
又
∵∠DGE=∠DCF=120°,
∴△DGE≌△DCF(ASA),
∴CF=GE.
∵AB=9,AE=2BE,
∴AE=6.
又
∵AG=AD=1/2AB=4.5,
∴EG=AE−AG=1.5,
∴CF=1.5.故选B

2. 如图,D是等边三角形ABC外一点,连接AD,BD,CD。已知AB= 4,AD= 4.5,∠BDC= 120°,则△BCD的周长为______。


答案:
8.5 点拨:如答图,延长BD至点E,使DE=CD,连接CE;
∵△ABC是等边三角形,
∴BC=AC=AB,∠ACB=60°.
∵∠BDC=120°,
∴∠CDE=60°.
又
∵DE=CD,
∴△CDE是等边三角形,
∴CE=CD,∠DCE=60°.
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE.
在△BCE和△ACD中,{BC=AC,∠BCE=∠ACD,CE=CD,
∴△BCE≌△ACD(SAS).
∴BE=AD=4.5,
∴BD+CD=4.5.
∵AB=4,
∴BC=4,
∴△BCD的周长=BC+BD+CD=4+4.5=8.5.

8.5 点拨:如答图,延长BD至点E,使DE=CD,连接CE;
∵△ABC是等边三角形,
∴BC=AC=AB,∠ACB=60°.
∵∠BDC=120°,
∴∠CDE=60°.
又
∵DE=CD,
∴△CDE是等边三角形,
∴CE=CD,∠DCE=60°.
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE.
在△BCE和△ACD中,{BC=AC,∠BCE=∠ACD,CE=CD,
∴△BCE≌△ACD(SAS).
∴BE=AD=4.5,
∴BD+CD=4.5.
∵AB=4,
∴BC=4,
∴△BCD的周长=BC+BD+CD=4+4.5=8.5.

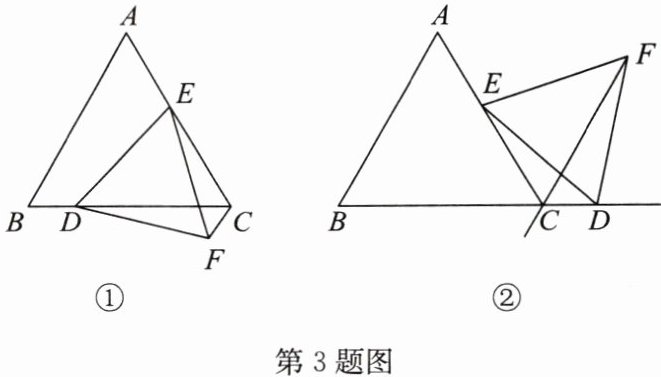
3. 如图,在等边三角形ABC中,E是边AC上一定点,D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF。
(1)如图①,若点D在边BC上,求证:CE+CF= CD;
(2)如图②,若点D在边BC的延长线上,请探究线段CE,CF与CD之间的数量关系,并说明理由。
(1)如图①,若点D在边BC上,求证:CE+CF= CD;
(2)如图②,若点D在边BC的延长线上,请探究线段CE,CF与CD之间的数量关系,并说明理由。

答案:
(1)证明:如答图①,过点E作EH//AB交BC于点H.
∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°.
∵EH//AB,
∴∠CEH=∠A=60°,∠CHE=∠B=60°,
∴∠CEH=∠CHE=∠HCE,
∴△CEH是等边三角形,
∴EC=EH=HC.
∵△DEF是等边三角形,
∴∠DEF=60°=∠HEC,ED=EF,
∴∠DEH=∠FEC,
∴△DEH≌△FEC(SAS),
∴CF=DH.
∵CD=CH+HD,
∴CE+CF=CD.
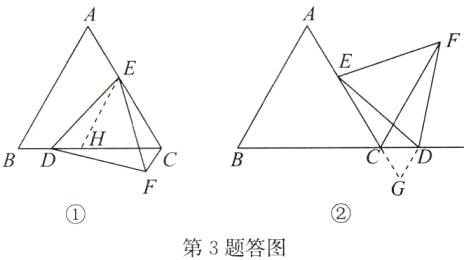
(2)解:CF=CD+CE,理由如下:
如答图②,过点D作DG//AB交AC的延长线于点G.同
(1)可证△CDG是等边三角形,
∴CD=CG=DG,∠CDG=60°.
∵△DEF是等边三角形,
∴∠EDF=60°=∠CDG,ED=FD.
∴∠FDC=∠EDG.
∴△EDG≌△FDC(SAS).
∴EG=FC;
∵EG=CG+CE,
∴CF=CD+CE;

(1)证明:如答图①,过点E作EH//AB交BC于点H.
∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°.
∵EH//AB,
∴∠CEH=∠A=60°,∠CHE=∠B=60°,
∴∠CEH=∠CHE=∠HCE,
∴△CEH是等边三角形,
∴EC=EH=HC.
∵△DEF是等边三角形,
∴∠DEF=60°=∠HEC,ED=EF,
∴∠DEH=∠FEC,
∴△DEH≌△FEC(SAS),
∴CF=DH.
∵CD=CH+HD,
∴CE+CF=CD.

(2)解:CF=CD+CE,理由如下:
如答图②,过点D作DG//AB交AC的延长线于点G.同
(1)可证△CDG是等边三角形,
∴CD=CG=DG,∠CDG=60°.
∵△DEF是等边三角形,
∴∠EDF=60°=∠CDG,ED=FD.
∴∠FDC=∠EDG.
∴△EDG≌△FDC(SAS).
∴EG=FC;
∵EG=CG+CE,
∴CF=CD+CE;
