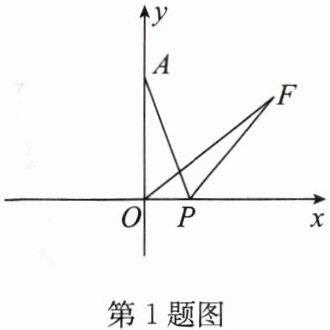
1. 如图,在平面直角坐标系中,点 A 的坐标为$(0,4)$,P 是 x 轴上一动点,把线段 PA 绕点 P 按顺时针方向旋转$60^{\circ }$得到线段 PF,连接 OF,则线段 OF 长的最小值是______.

答案:
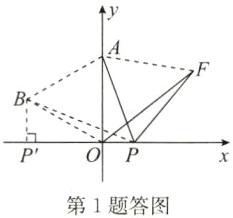
2 点拨:如答图,在第二象限作等边三角形AOB,连接BP,AF,过点B作BP'⊥x轴于点P',易得△APF为等边三角形,可证△BAP≌△OAF,得出BP=OF.当BP⊥x轴,即点P与点P'重合时,BP的长取得最小值.在Rt△BP'O中,∠BOP'=90° - ∠AOB=30°,
∴易得BP'=$\frac{1}{2}$OB=$\frac{1}{2}$×4=2,即BP长的最小值为2,
∴OF长的最小值为2.
2 点拨:如答图,在第二象限作等边三角形AOB,连接BP,AF,过点B作BP'⊥x轴于点P',易得△APF为等边三角形,可证△BAP≌△OAF,得出BP=OF.当BP⊥x轴,即点P与点P'重合时,BP的长取得最小值.在Rt△BP'O中,∠BOP'=90° - ∠AOB=30°,
∴易得BP'=$\frac{1}{2}$OB=$\frac{1}{2}$×4=2,即BP长的最小值为2,
∴OF长的最小值为2.

2. 阅读下列一段文字,回答问题.
【材料阅读】平面内两点$M(x_{1},y_{1}),N(x_{2},y_{2})$,则由勾股定理可得,这两点间的距离为$MN= \sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}$.
例如,已知点$M(3,1),N(1,-2)$,则$MN= \sqrt {(3-1)^{2}+(1+2)^{2}}= \sqrt {13}$.
(1)【知识理解】已知点$P(2,4),Q(-3,-8)$,求 P,Q 两点间的距离;
(2)【知识运用】已知点$A(1,2),B(4,-2)$,O 是坐标原点,判断$\triangle AOB$是什么三角形,并说明理由;
(3)【知识迁移】借助上面的思考过程,建立几何模型,求$\sqrt {x^{2}+9}+\sqrt {(16-x)^{2}+81}$的最小值.
【材料阅读】平面内两点$M(x_{1},y_{1}),N(x_{2},y_{2})$,则由勾股定理可得,这两点间的距离为$MN= \sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}$.
例如,已知点$M(3,1),N(1,-2)$,则$MN= \sqrt {(3-1)^{2}+(1+2)^{2}}= \sqrt {13}$.
(1)【知识理解】已知点$P(2,4),Q(-3,-8)$,求 P,Q 两点间的距离;
(2)【知识运用】已知点$A(1,2),B(4,-2)$,O 是坐标原点,判断$\triangle AOB$是什么三角形,并说明理由;
(3)【知识迁移】借助上面的思考过程,建立几何模型,求$\sqrt {x^{2}+9}+\sqrt {(16-x)^{2}+81}$的最小值.
答案:解:
(1)PQ=$\sqrt{(-3 - 2)^{2}+(-8 - 4)^{2}}$=13.
(2)△AOB是直角三角形,理由:
∵A(1,2),O(0,0),B(4, - 2),
∴OA=$\sqrt{(0 - 1)^{2}+(0 - 2)^{2}}$=$\sqrt{5}$,
OB=$\sqrt{(0 - 4)^{2}+(0 + 2)^{2}}$=$\sqrt{20}$,
AB=$\sqrt{(4 - 1)^{2}+(-2 - 2)^{2}}$=5.
∴OA²+OB²=5 + 20=25,AB²=25.
∴OA²+OB²=AB²,
∴△AOB是直角三角形.
(3)
∵$\sqrt{x^{2}+9}$=$\sqrt{x^{2}+3^{2}}$,$\sqrt{(16 - x)^{2}+81}$=$\sqrt{(16 - x)^{2}+9^{2}}$=$\sqrt{(16 - x)^{2}+(12 - 3)^{2}}$,
∴可设C(x,3),D(16,12),O(0,0),
则OC=$\sqrt{x^{2}+9}$,CD=$\sqrt{(16 - x)^{2}+81}$.
∴$\sqrt{x^{2}+9}$+$\sqrt{(16 - x)^{2}+81}$的最小值为OD,此时O,C,D在同一条直线上,
∴OD=$\sqrt{16^{2}+12^{2}}$=20,
即$\sqrt{x^{2}+9}$+$\sqrt{(16 - x)^{2}+81}$的最小值为20.
(1)PQ=$\sqrt{(-3 - 2)^{2}+(-8 - 4)^{2}}$=13.
(2)△AOB是直角三角形,理由:
∵A(1,2),O(0,0),B(4, - 2),
∴OA=$\sqrt{(0 - 1)^{2}+(0 - 2)^{2}}$=$\sqrt{5}$,
OB=$\sqrt{(0 - 4)^{2}+(0 + 2)^{2}}$=$\sqrt{20}$,
AB=$\sqrt{(4 - 1)^{2}+(-2 - 2)^{2}}$=5.
∴OA²+OB²=5 + 20=25,AB²=25.
∴OA²+OB²=AB²,
∴△AOB是直角三角形.
(3)
∵$\sqrt{x^{2}+9}$=$\sqrt{x^{2}+3^{2}}$,$\sqrt{(16 - x)^{2}+81}$=$\sqrt{(16 - x)^{2}+9^{2}}$=$\sqrt{(16 - x)^{2}+(12 - 3)^{2}}$,
∴可设C(x,3),D(16,12),O(0,0),
则OC=$\sqrt{x^{2}+9}$,CD=$\sqrt{(16 - x)^{2}+81}$.
∴$\sqrt{x^{2}+9}$+$\sqrt{(16 - x)^{2}+81}$的最小值为OD,此时O,C,D在同一条直线上,
∴OD=$\sqrt{16^{2}+12^{2}}$=20,
即$\sqrt{x^{2}+9}$+$\sqrt{(16 - x)^{2}+81}$的最小值为20.