1. 如图,已知$C是线段AB$上一点,$\angle DCE = \angle A = \angle B$,$CD = CE$.猜想$AB$,$AD$,$BE$之间的数量关系为
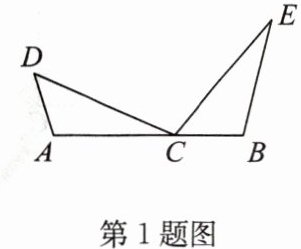
AB=AD+BE
.
答案:AB=AD+BE 点拨:
∵∠A+∠D+∠ACD=∠ACD+∠DCE+∠ECB=180°,∠DCE=∠A,
∴∠D=∠BCE.又
∵∠A=∠B,CD=EC,
∴△ACD≌△BEC(AAS).
∴AD=BC,AC=BE.
∵AB=AC+BC,
∴AB=AD+BE.
∵∠A+∠D+∠ACD=∠ACD+∠DCE+∠ECB=180°,∠DCE=∠A,
∴∠D=∠BCE.又
∵∠A=∠B,CD=EC,
∴△ACD≌△BEC(AAS).
∴AD=BC,AC=BE.
∵AB=AC+BC,
∴AB=AD+BE.
2. 如图,在$\triangle ABC$中,$AB = AC = 2$,$\angle B = \angle C = 40^{\circ}$,点$D在线段BC$上运动(不与点$B$,$C$重合),连接$AD$,作$\angle ADE = 40^{\circ}$,$DE交线段AC于点E$.
(1)当$\angle BDA = 115^{\circ}$时,$\angle EDC = $
(2)线段$DC$的长度为何值时,$\triangle ABD \cong \triangle DCE$?请说明理由.
(3)在点$D$的运动过程中,$\triangle ADE$的形状可以是等腰三角形吗?若可以,请求出$\angle BDA$的度数;若不可以,请说明理由.
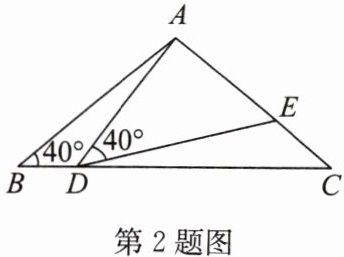
(1)当$\angle BDA = 115^{\circ}$时,$\angle EDC = $
25
$^{\circ}$,$\angle AED = $______65
$^{\circ}$.(2)线段$DC$的长度为何值时,$\triangle ABD \cong \triangle DCE$?请说明理由.
(3)在点$D$的运动过程中,$\triangle ADE$的形状可以是等腰三角形吗?若可以,请求出$\angle BDA$的度数;若不可以,请说明理由.

答案:
(1)25 65
(2)解:当DC=2时,△ABD≌△DCE,理由如下:
∵DC=2,AB=2,
∴AB=DC.
∵∠C=40°,
∴∠DEC+∠EDC=140°.
∵∠ADE=40°,
∴∠EDC+∠ADB=140°.
∴∠ADB=∠DEC.又
∵∠B=∠C,
∴△ABD≌△DCE(AAS).
(3)解:当∠BDA的度数为110°或80°时,△ADE是等腰三角形,理由如下:①当DA=DE时,∠DAE=∠DEA=70°,
∴∠BDA=∠DAE+∠C=70°+40°=110°.②当AD=AE时,∠AED=∠ADE=40°,
∴∠DAE=100°.此时点D与点B重合,不符合题意.③当EA=ED时,∠EDA=∠DAE=40°,
∴∠BDA=∠EAD+∠C=40°+40°=80°.综上,当∠BDA的度数为110°或80°时,△ADE是等腰三角形.
(1)25 65
(2)解:当DC=2时,△ABD≌△DCE,理由如下:
∵DC=2,AB=2,
∴AB=DC.
∵∠C=40°,
∴∠DEC+∠EDC=140°.
∵∠ADE=40°,
∴∠EDC+∠ADB=140°.
∴∠ADB=∠DEC.又
∵∠B=∠C,
∴△ABD≌△DCE(AAS).
(3)解:当∠BDA的度数为110°或80°时,△ADE是等腰三角形,理由如下:①当DA=DE时,∠DAE=∠DEA=70°,
∴∠BDA=∠DAE+∠C=70°+40°=110°.②当AD=AE时,∠AED=∠ADE=40°,
∴∠DAE=100°.此时点D与点B重合,不符合题意.③当EA=ED时,∠EDA=∠DAE=40°,
∴∠BDA=∠EAD+∠C=40°+40°=80°.综上,当∠BDA的度数为110°或80°时,△ADE是等腰三角形.