等腰三角形的判定定理:有
两个角
相等的三角形是等腰三角形(简称“等角对等边
”)。答案:两个角 等角对等边
1. 有下列长度的三条线段(单位:cm),能组成等腰三角形的是(
A.2,2,4
B.3,8,3
C.3,4,6
D.5,4,4
D
)A.2,2,4
B.3,8,3
C.3,4,6
D.5,4,4
答案:D
解析:
A. $2+2=4$,不能组成三角形;
B. $3+3=6<8$,不能组成三角形;
C. 三条线段互不相等,不能组成等腰三角形;
D. $4+4=8>5$,$5-4=1<4$,能组成等腰三角形。
D
B. $3+3=6<8$,不能组成三角形;
C. 三条线段互不相等,不能组成等腰三角形;
D. $4+4=8>5$,$5-4=1<4$,能组成等腰三角形。
D
2. 在△ABC 中,下列能判定△ABC 为等腰三角形的是(
A.∠A = 40°,∠B = 50°
B.∠A = 40°,∠B = 60°
C.∠A = 40°,∠B = 70°
D.∠A = 40°,∠B = 80°
C
)A.∠A = 40°,∠B = 50°
B.∠A = 40°,∠B = 60°
C.∠A = 40°,∠B = 70°
D.∠A = 40°,∠B = 80°
答案:C
解析:
在△ABC中,三角形内角和为180°。
选项A:∠A=40°,∠B=50°,则∠C=180°-40°-50°=90°,三个角均不相等,不是等腰三角形。
选项B:∠A=40°,∠B=60°,则∠C=180°-40°-60°=80°,三个角均不相等,不是等腰三角形。
选项C:∠A=40°,∠B=70°,则∠C=180°-40°-70°=70°,∠B=∠C,所以△ABC为等腰三角形。
选项D:∠A=40°,∠B=80°,则∠C=180°-40°-80°=60°,三个角均不相等,不是等腰三角形。
C
选项A:∠A=40°,∠B=50°,则∠C=180°-40°-50°=90°,三个角均不相等,不是等腰三角形。
选项B:∠A=40°,∠B=60°,则∠C=180°-40°-60°=80°,三个角均不相等,不是等腰三角形。
选项C:∠A=40°,∠B=70°,则∠C=180°-40°-70°=70°,∠B=∠C,所以△ABC为等腰三角形。
选项D:∠A=40°,∠B=80°,则∠C=180°-40°-80°=60°,三个角均不相等,不是等腰三角形。
C
3. 在△ABC 中,∠A = 100°,当∠B =
40
°时,△ABC 是等腰三角形。答案:40
解析:
当∠A为顶角时,∠B=∠C,∠B=(180°-100°)/2=40°;当∠A为底角时,∠A=∠B=100°,此时∠A+∠B=200°>180°,不成立。故∠B=40°。
4. 如图,∠A = 36°,∠DBC = 36°,∠C = 72°,则等腰三角形有
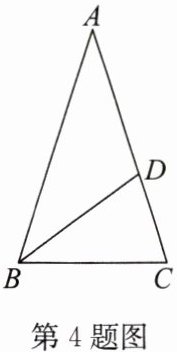
3
个。
答案:3
解析:
解:在△ABC中,∠A=36°,∠C=72°,
∠ABC=180°-∠A-∠C=72°,
∠ABC=∠C,△ABC是等腰三角形。
在△DBC中,∠DBC=36°,∠C=72°,
∠BDC=180°-∠DBC-∠C=72°,
∠BDC=∠C,△DBC是等腰三角形。
∠ABD=∠ABC-∠DBC=72°-36°=36°,
∠ABD=∠A,△ABD是等腰三角形。
综上,等腰三角形有3个。
答案:3
∠ABC=180°-∠A-∠C=72°,
∠ABC=∠C,△ABC是等腰三角形。
在△DBC中,∠DBC=36°,∠C=72°,
∠BDC=180°-∠DBC-∠C=72°,
∠BDC=∠C,△DBC是等腰三角形。
∠ABD=∠ABC-∠DBC=72°-36°=36°,
∠ABD=∠A,△ABD是等腰三角形。
综上,等腰三角形有3个。
答案:3
5. 如图,AD 是△ABC 中∠BAC 的平分线,CE//AD 交 BA 的延长线于点 E。求证:△ACE 是等腰三角形。
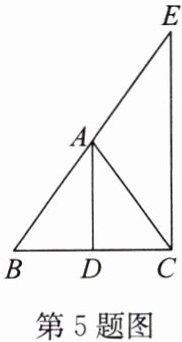

答案:证明:
∵AD是△ABC中∠BAC的平分线,
∴∠BAD=∠CAD.
∵CE//AD,
∴∠BAD=∠E,∠ACE=∠CAD.
∴∠E=∠ACE,
∴AC=AE,即△ACE是等腰三角形.
∵AD是△ABC中∠BAC的平分线,
∴∠BAD=∠CAD.
∵CE//AD,
∴∠BAD=∠E,∠ACE=∠CAD.
∴∠E=∠ACE,
∴AC=AE,即△ACE是等腰三角形.
6. 如图,点 B,C 在 AD 上,AB = CD,∠A = ∠D,∠F = ∠E,BE,CF 交于点 O。求证:OE = OF。
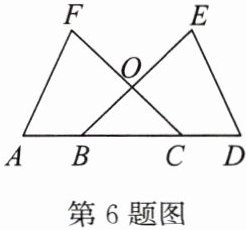

答案:证明:
∵AB=CD,
∴AB+BC=CD+BC,即AC=DB.又
∵∠A=∠D,∠F=∠E,
∴△ACF≌△DBE(AAS).
∴CF=BE,∠ACF=∠DBE.
∴OC=OB,
∴CF-OC=BE-OB,即OE=OF.
∵AB=CD,
∴AB+BC=CD+BC,即AC=DB.又
∵∠A=∠D,∠F=∠E,
∴△ACF≌△DBE(AAS).
∴CF=BE,∠ACF=∠DBE.
∴OC=OB,
∴CF-OC=BE-OB,即OE=OF.