1.
有理数
和______无理数
统称为实数.答案:有理数 无理数
2. 实数
0
正实数
0
负实数
答案:正实数 负实数
3.
实
数与数轴上的点一一对应.答案:实
4. 数轴上的任意两个点,
右边
的点表示的实数比左边
的点表示的实数大.答案:右边 左边
1. 下列四个实数中最小的是(
A.$-\sqrt{5}$
B.$-2$
C.$0$
D.$\sqrt{2}$
A
)A.$-\sqrt{5}$
B.$-2$
C.$0$
D.$\sqrt{2}$
答案:A
2. 与$\sqrt{37}$最接近的整数是(
A.$5$
B.$6$
C.$6.5$
D.$7$
B
)A.$5$
B.$6$
C.$6.5$
D.$7$
答案:B
解析:
因为$6^2 = 36$,$7^2 = 49$,所以$6 < \sqrt{37} < 7$。
$\sqrt{37} - 6$与$7 - \sqrt{37}$比较大小:
$\sqrt{37} - 6$,$7 - \sqrt{37}$,
$(\sqrt{37} - 6) - (7 - \sqrt{37}) = 2\sqrt{37} - 13$,
$\sqrt{37} \approx 6.08$,$2\sqrt{37} \approx 12.16$,$12.16 - 13 = -0.84 < 0$,
所以$\sqrt{37} - 6 < 7 - \sqrt{37}$,即$\sqrt{37}$更接近$6$。
B
$\sqrt{37} - 6$与$7 - \sqrt{37}$比较大小:
$\sqrt{37} - 6$,$7 - \sqrt{37}$,
$(\sqrt{37} - 6) - (7 - \sqrt{37}) = 2\sqrt{37} - 13$,
$\sqrt{37} \approx 6.08$,$2\sqrt{37} \approx 12.16$,$12.16 - 13 = -0.84 < 0$,
所以$\sqrt{37} - 6 < 7 - \sqrt{37}$,即$\sqrt{37}$更接近$6$。
B
3. 关于$\sqrt{19}$,下列说法不正确的是(
A.它是一个无理数
B.它可以用数轴上的一个点来表示
C.它可以表示面积为 19 的正方形的边长
D.若$n < \sqrt{19} < n + 1$($n$为整数),则$n = 5$
D
)A.它是一个无理数
B.它可以用数轴上的一个点来表示
C.它可以表示面积为 19 的正方形的边长
D.若$n < \sqrt{19} < n + 1$($n$为整数),则$n = 5$
答案:D
4. 若将三个数$-\sqrt{3}$,$\sqrt{7}$,$\sqrt{13}$表示在数轴上,其中一个数被墨迹覆盖(如图),则这个被覆盖的数是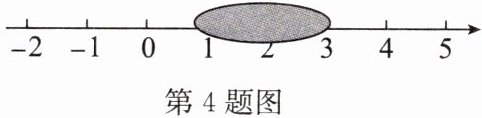
$\sqrt{7}$
.
答案:$\sqrt{7}$
解析:
解:$\because -\sqrt{3}\approx -1.732$,$2<\sqrt{7}<3$,$3<\sqrt{13}<4$,
数轴上墨迹覆盖范围在$1$到$3$之间,
$\therefore$被覆盖的数是$\sqrt{7}$。
$\sqrt{7}$
数轴上墨迹覆盖范围在$1$到$3$之间,
$\therefore$被覆盖的数是$\sqrt{7}$。
$\sqrt{7}$
5. 下列实数:$\sqrt{144}$,$-\frac{22}{7}$,$3 - \pi$,$\sqrt{0.4}$,$0$,$3.14$,$\sqrt[3]{-64}$,$(\pi + 1)^0$,$-\sqrt{2}$,$0.1010010001$,其中无理数有
3
个,负实数有4
个.答案:3 4
解析:
无理数:$3 - \pi$,$\sqrt{0.4}$,$-\sqrt{2}$,共3个;
负实数:$-\frac{22}{7}$,$3 - \pi$,$\sqrt[3]{-64}$,$-\sqrt{2}$,共4个.
3 4
负实数:$-\frac{22}{7}$,$3 - \pi$,$\sqrt[3]{-64}$,$-\sqrt{2}$,共4个.
3 4
6. 实数$a$,$b$在数轴上的对应点的位置如图所示,化简$|a + b| + | - a| + \sqrt[3]{b^3}$.


答案:解:原式$=-(a+b)-a+b=-a-b-a+b=-2a$.
解析:
解:由数轴可知$a<0$,$b>0$,且$|a|>|b|$,则$a + b<0$,$-a>0$。
原式$=-(a + b)+(-a)+b$
$=-a - b - a + b$
$=-2a$。
原式$=-(a + b)+(-a)+b$
$=-a - b - a + b$
$=-2a$。
7. 计算:
(1) $-1^2×(3 - \pi)^0 - \sqrt[3]{8} + (\frac{1}{2})^{-1}$;
(2) $\sqrt{25} - \sqrt[3]{64} - (-1)^{2024} + |\sqrt{3} - 2|$.
(1) $-1^2×(3 - \pi)^0 - \sqrt[3]{8} + (\frac{1}{2})^{-1}$;
(2) $\sqrt{25} - \sqrt[3]{64} - (-1)^{2024} + |\sqrt{3} - 2|$.
答案:$(1)$ 计算$-1^2×(3 - \pi)^0 - \sqrt[3]{8} + (\frac{1}{2})^{-1}$
解:
根据幂运算规则:$a^0 = 1(a\neq0)$,$a^{-p}=\frac{1}{a^p}(a\neq0)$,$\sqrt[3]{a^3}=a$。
计算$-1^2$:根据运算顺序,先计算指数,$-1^2=- (1×1)= - 1$;
计算$(3 - \pi)^0$:因为$3-\pi\neq0$,所以$(3 - \pi)^0 = 1$;
计算$\sqrt[3]{8}$:因为$2^3 = 8$,所以$\sqrt[3]{8}=2$;
计算$(\frac{1}{2})^{-1}$:根据$a^{-p}=\frac{1}{a^p}$,则$(\frac{1}{2})^{-1}=\frac{1}{\frac{1}{2}} = 2$。
将上述结果代入原式可得:
$\begin{aligned}&-1^2×(3 - \pi)^0 - \sqrt[3]{8} + (\frac{1}{2})^{-1}\\=&-1×1 - 2 + 2\\=&-1+( - 2 + 2)\\=&-1+0\\=&-1\end{aligned}$
$(2)$ 计算$\sqrt{25} - \sqrt[3]{64} - (-1)^{2024} + |\sqrt{3} - 2|$
解:
根据根式运算规则:$\sqrt{a^2}=|a|$($a\geq0$时,$\sqrt{a^2}=a$),$\sqrt[3]{a^3}=a$,绝对值的性质:当$a\lt b$时,$|a - b|=b - a$。
计算$\sqrt{25}$:因为$5^2 = 25$,所以$\sqrt{25}=5$;
计算$\sqrt[3]{64}$:因为$4^3 = 64$,所以$\sqrt[3]{64}=4$;
计算$(-1)^{2024}$:因为$2024$是偶数,所以$(-1)^{2024}=1$;
计算$|\sqrt{3} - 2|$:因为$\sqrt{3}\lt2$,所以$|\sqrt{3} - 2|=2 - \sqrt{3}$。
将上述结果代入原式可得:
$\begin{aligned}&\sqrt{25} - \sqrt[3]{64} - (-1)^{2024} + |\sqrt{3} - 2|\\=&5 - 4 - 1+(2 - \sqrt{3})\\=&(5 - 4 - 1)+2 - \sqrt{3}\\=&0 + 2 - \sqrt{3}\\=&2 - \sqrt{3}\end{aligned}$
综上,$(1)$的结果为$-1$;$(2)$的结果为$2 - \sqrt{3}$。
解:
根据幂运算规则:$a^0 = 1(a\neq0)$,$a^{-p}=\frac{1}{a^p}(a\neq0)$,$\sqrt[3]{a^3}=a$。
计算$-1^2$:根据运算顺序,先计算指数,$-1^2=- (1×1)= - 1$;
计算$(3 - \pi)^0$:因为$3-\pi\neq0$,所以$(3 - \pi)^0 = 1$;
计算$\sqrt[3]{8}$:因为$2^3 = 8$,所以$\sqrt[3]{8}=2$;
计算$(\frac{1}{2})^{-1}$:根据$a^{-p}=\frac{1}{a^p}$,则$(\frac{1}{2})^{-1}=\frac{1}{\frac{1}{2}} = 2$。
将上述结果代入原式可得:
$\begin{aligned}&-1^2×(3 - \pi)^0 - \sqrt[3]{8} + (\frac{1}{2})^{-1}\\=&-1×1 - 2 + 2\\=&-1+( - 2 + 2)\\=&-1+0\\=&-1\end{aligned}$
$(2)$ 计算$\sqrt{25} - \sqrt[3]{64} - (-1)^{2024} + |\sqrt{3} - 2|$
解:
根据根式运算规则:$\sqrt{a^2}=|a|$($a\geq0$时,$\sqrt{a^2}=a$),$\sqrt[3]{a^3}=a$,绝对值的性质:当$a\lt b$时,$|a - b|=b - a$。
计算$\sqrt{25}$:因为$5^2 = 25$,所以$\sqrt{25}=5$;
计算$\sqrt[3]{64}$:因为$4^3 = 64$,所以$\sqrt[3]{64}=4$;
计算$(-1)^{2024}$:因为$2024$是偶数,所以$(-1)^{2024}=1$;
计算$|\sqrt{3} - 2|$:因为$\sqrt{3}\lt2$,所以$|\sqrt{3} - 2|=2 - \sqrt{3}$。
将上述结果代入原式可得:
$\begin{aligned}&\sqrt{25} - \sqrt[3]{64} - (-1)^{2024} + |\sqrt{3} - 2|\\=&5 - 4 - 1+(2 - \sqrt{3})\\=&(5 - 4 - 1)+2 - \sqrt{3}\\=&0 + 2 - \sqrt{3}\\=&2 - \sqrt{3}\end{aligned}$
综上,$(1)$的结果为$-1$;$(2)$的结果为$2 - \sqrt{3}$。