1. 一般地,一次函数 $ y = kx + b(k \neq 0) $ 图象上任意一点的坐标都是二元一次方程
kx-y+b=0
的解,以二元一次方程 $ kx - y + b = 0 $ 的解为坐标的点都在一次函数y=kx+b
的图象上.答案:kx-y+b=0 y=kx+b
2. 一般地,如果两个一次函数的图象有一个交点,那么交点的坐标就是相应的
二元一次方程组
的解.答案:二元一次方程组
1. 把二元一次方程 $ 3x + 2y - 4 = 0 $ 改写成 $ y $ 关于 $ x $ 的函数表达式为(
A.$ y = - 3x + 4 $
B.$ y = - \frac{3}{2}x - 2 $
C.$ y = - \frac{3}{2}x + 2 $
D.$ y = x - 4 $
C
)A.$ y = - 3x + 4 $
B.$ y = - \frac{3}{2}x - 2 $
C.$ y = - \frac{3}{2}x + 2 $
D.$ y = x - 4 $
答案:C
解析:
$3x + 2y - 4 = 0$
$2y = -3x + 4$
$y = -\frac{3}{2}x + 2$
C
$2y = -3x + 4$
$y = -\frac{3}{2}x + 2$
C
2. 在同一平面直角坐标系中,直线 $ y = 2x + 1 $ 与直线 $ y = - 3x + b $ 的交点不可能在(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:D
解析:
联立两直线方程:$\begin{cases}y = 2x + 1 \\ y = -3x + b\end{cases}$
解得:$x = \frac{b - 1}{5}$,$y = \frac{2b + 3}{5}$
直线$y = 2x + 1$过第一、二、三象限。
当交点在第四象限时,需$\begin{cases}\frac{b - 1}{5} > 0 \\ \frac{2b + 3}{5} < 0\end{cases}$
由$\frac{b - 1}{5} > 0$得$b > 1$;由$\frac{2b + 3}{5} < 0$得$b < -\frac{3}{2}$,矛盾。
故交点不可能在第四象限。
D
解得:$x = \frac{b - 1}{5}$,$y = \frac{2b + 3}{5}$
直线$y = 2x + 1$过第一、二、三象限。
当交点在第四象限时,需$\begin{cases}\frac{b - 1}{5} > 0 \\ \frac{2b + 3}{5} < 0\end{cases}$
由$\frac{b - 1}{5} > 0$得$b > 1$;由$\frac{2b + 3}{5} < 0$得$b < -\frac{3}{2}$,矛盾。
故交点不可能在第四象限。
D
3. 已知一次函数 $ y = 3x - 1 $ 与 $ y = kx $($ k $ 是常数,$ k \neq 0 $)的图象的交点坐标是 $ (-1, - 4) $,则方程组 $ \begin{cases} 3x - y - 1 = 0, \\ kx - y = 0 \end{cases} $ 的解是
$\begin{cases} x=-1 \\ y=-4 \end{cases}$
.答案:{x=-1 y=-4
解析:
$\begin{cases} x=-1 \\ y=-4 \end{cases}$
4. 直线 $ y = - x - 2 $ 与直线 $ y = x + 6 $ 的交点坐标为
(-4,2)
.答案:(-4,2)
解析:
解:联立方程组$\begin{cases}y=-x-2\\y=x+6\end{cases}$
将$y=x+6$代入$y=-x-2$,得$x+6=-x-2$
移项得$x+x=-2-6$
合并同类项得$2x=-8$
解得$x=-4$
将$x=-4$代入$y=x+6$,得$y=-4+6=2$
交点坐标为$(-4,2)$
将$y=x+6$代入$y=-x-2$,得$x+6=-x-2$
移项得$x+x=-2-6$
合并同类项得$2x=-8$
解得$x=-4$
将$x=-4$代入$y=x+6$,得$y=-4+6=2$
交点坐标为$(-4,2)$
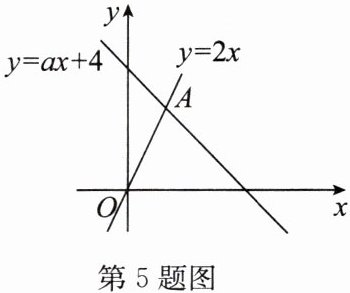
5. 如图,直线 $ y = 2x $ 和直线 $ y = ax + 4 $ 相交于点 $ A(m, 3) $.
(1) 求 $ m $ 的值;
(2) 观察图象,直接写出关于 $ x $,$ y $ 的方程组 $ \begin{cases} y = 2x, \\ y = ax + 4 \end{cases} $ 的解.
(1) 求 $ m $ 的值;
(2) 观察图象,直接写出关于 $ x $,$ y $ 的方程组 $ \begin{cases} y = 2x, \\ y = ax + 4 \end{cases} $ 的解.

答案:解:
(1)
∵直线y=2x和直线y=ax+4相交于点A(m,3),
∴2m=3,解得m=3/2.
(2){x=3/2, y=3.
(1)
∵直线y=2x和直线y=ax+4相交于点A(m,3),
∴2m=3,解得m=3/2.
(2){x=3/2, y=3.
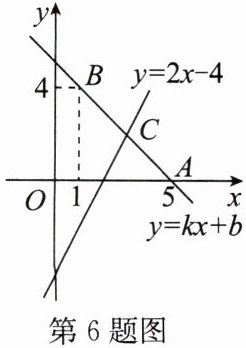
6. 如图,已知直线 $ y = kx + b $ 经过点 $ A(5, 0) $,$ B(1, 4) $,直线 $ y = 2x - 4 $ 与该直线交于点 $ C $.
(1) 求直线 $ AB $ 的函数表达式;
(2) 求点 $ C $ 的坐标.
(1) 求直线 $ AB $ 的函数表达式;
(2) 求点 $ C $ 的坐标.

答案:解:
(1)根据题意,得{5k+b=0, k+b=4, 解得{k=-1, b=5.
∴直线AB的函数表达式为y=-x+5.
(2)由题意,得{y=-x+5, y=2x-4, 解得{x=3, y=2,故点C的坐标为(3,2).
(1)根据题意,得{5k+b=0, k+b=4, 解得{k=-1, b=5.
∴直线AB的函数表达式为y=-x+5.
(2)由题意,得{y=-x+5, y=2x-4, 解得{x=3, y=2,故点C的坐标为(3,2).