1. 如图,求直角三角形未知边的长度。
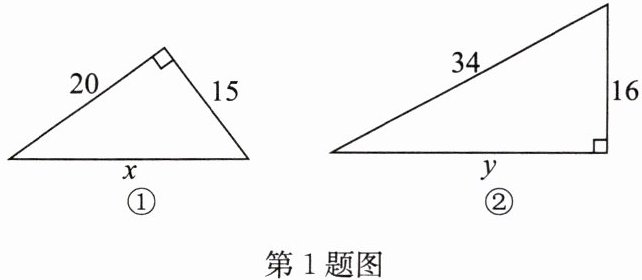

答案:解:①由勾股定理得$x^{2}=20^{2}+15^{2}$,解得$x=\pm 25$,
∵x表示边长,
∴$x=25$.②由勾股定理得$y^{2}=34^{2}-16^{2}$,解得$y=\pm 30$,
∵y表示边长,
∴$y=30$.
∵x表示边长,
∴$x=25$.②由勾股定理得$y^{2}=34^{2}-16^{2}$,解得$y=\pm 30$,
∵y表示边长,
∴$y=30$.
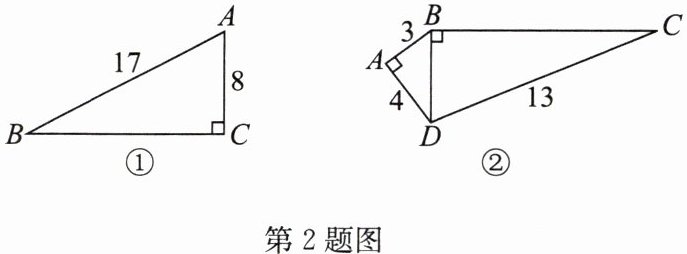
2. 根据所给条件,解决下列问题。
(1) 求图①中 $ BC $ 边的长;
(2) 求图②中 $ BC $ 边的长。
(1) 求图①中 $ BC $ 边的长;
(2) 求图②中 $ BC $ 边的长。

答案:解:
(1)
∵$BC^{2}=AB^{2}-AC^{2}=17^{2}-8^{2}=225$,
∴$BC=15$.
(2)
∵$BD^{2}=AB^{2}+AD^{2}=3^{2}+4^{2}=25$,
∴$BD=5$,
∴$BC^{2}=CD^{2}-BD^{2}=13^{2}-5^{2}=144$,
∴$BC=12$.
(1)
∵$BC^{2}=AB^{2}-AC^{2}=17^{2}-8^{2}=225$,
∴$BC=15$.
(2)
∵$BD^{2}=AB^{2}+AD^{2}=3^{2}+4^{2}=25$,
∴$BD=5$,
∴$BC^{2}=CD^{2}-BD^{2}=13^{2}-5^{2}=144$,
∴$BC=12$.
3. 如图,点 $ E $ 在正方形 $ ABCD $ 的边 $ AB $ 上,若 $ EB = 6 $,$ EC = 10 $,求正方形 $ ABCD $ 的面积。
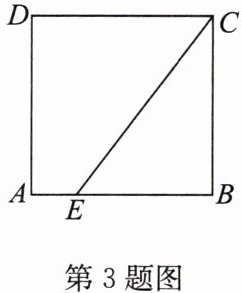

答案:解:由勾股定理得$BC^{2}=CE^{2}-BE^{2}=10^{2}-6^{2}=64$,
∴正方形ABCD的面积$=BC^{2}=64$.
∴正方形ABCD的面积$=BC^{2}=64$.
4. 已知 $ \triangle ABC $ 的三边长分别为 $ 5 $,$ x - 2 $,$ x + 1 $。若该三角形是以 $ x + 1 $ 为斜边的直角三角形,求 $ x $ 的值。
答案:解:由题意得$5^{2}+(x-2)^{2}=(x+1)^{2}$,整理,得$6x=28$,解得$x=\frac{14}{3}$.
∴x的值为$\frac{14}{3}$.
∴x的值为$\frac{14}{3}$.
5. 在 $ Rt\triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ a $,$ b $,$ c $ 分别是 $ \angle A $,$ \angle B $,$ \angle C $ 对应的边长。若 $ c = 10\ cm $,$ a : b = 3 : 4 $,求 $ \triangle ABC $ 的周长。
答案:解:
∵$a:b=3:4$,
∴设$a=3x\ cm$,$b=4x\ cm$.
∵$\angle C=90^{\circ}$,
∴$a^{2}+b^{2}=c^{2}$,即$(3x)^{2}+(4x)^{2}=10^{2}$,
∴$x=2$.
∴$a=6\ cm$,$b=8\ cm$.
∴$\triangle ABC$的周长为$6+8+10=24(cm)$.
∵$a:b=3:4$,
∴设$a=3x\ cm$,$b=4x\ cm$.
∵$\angle C=90^{\circ}$,
∴$a^{2}+b^{2}=c^{2}$,即$(3x)^{2}+(4x)^{2}=10^{2}$,
∴$x=2$.
∴$a=6\ cm$,$b=8\ cm$.
∴$\triangle ABC$的周长为$6+8+10=24(cm)$.