29. 如图(a)所示,某人用滑轮组提水。他在20s的时间内把重为120N的水从井中匀速提升了5m,拉力所做的功W随时间t的变化图像如图(b)所示。求:
(1)此人在20s内所做的有用功。
(2)滑轮组的机械效率。
(3)拉力的大小。
(4)拉力的功率。
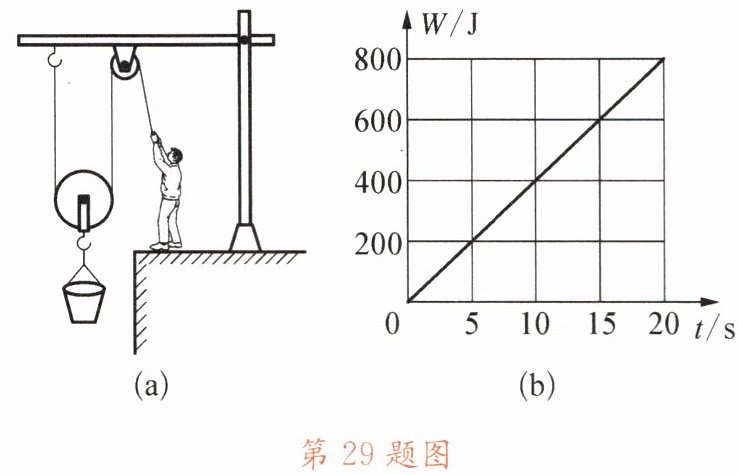
(1)此人在20s内所做的有用功。
(2)滑轮组的机械效率。
(3)拉力的大小。
(4)拉力的功率。

答案:(1)600J (2)75% (3)80N (4)40W
解析:
(1)有用功$W_{有}=Gh=120\,N × 5\,m=600\,J$
(2)由图(b)知总功$W_{总}=800\,J$,机械效率$\eta=\frac{W_{有}}{W_{总}} × 100\%=\frac{600\,J}{800\,J} × 100\% =75\%$
(3)由图(a)知$n=2$,绳端移动距离$s=nh=2 × 5\,m=10\,m$,拉力$F=\frac{W_{总}}{s}=\frac{800\,J}{10\,m}=80\,N$
(4)拉力功率$P=\frac{W_{总}}{t}=\frac{800\,J}{20\,s}=40\,W$
30. 某同学用图示的牵引装置来锻炼关节的功能。重物质量为3kg,小腿拉绳使重物在4s内匀速上升0.5m。若不计绳重及摩擦,求:
(1)小腿拉重物所做的功。
(2)小腿拉重物的功率。

(1)小腿拉重物所做的功。
(2)小腿拉重物的功率。

答案:(1)15J (2)3.75W
解析:
(1)因为不计绳重及摩擦,小腿拉重物所做的功等于克服重物重力做的功。重物质量$m = 3\space kg$,重力$G=mg=3\space kg×10\space N/kg = 30\space N$,上升高度$h = 0.5\space m$,所以功$W=Gh=30\space N×0.5\space m = 15\space J$。
(2)时间$t = 4\space s$,功率$P=\frac{W}{t}=\frac{15\space J}{4\space s}=3.75\space W$。
31. 塔吊是建筑工地上普遍使用的起重设备。如图所示的塔吊,AB是竖直支架,CD是水平臂,其上OC段叫平衡臂,C端装有配重体,OD段叫吊臂,E为滑轮组(可在O、D两点间移动)。设滑轮组重力及摩擦忽略不计。
(1)当OE= 15m时,若用此塔吊能起吊重物的最大质量是0.8t,则当滑轮组移到D点(OD= 25m)时,能够安全起吊重物的最大质量是多少?
(2)当OE= 15m时,用此塔吊将0.8t的钢材先竖直匀速吊起8m,然后沿水平方向缓缓移动4m,送达指定位置。在这一过程中,塔吊对钢材做了多少功?

(1)当OE= 15m时,若用此塔吊能起吊重物的最大质量是0.8t,则当滑轮组移到D点(OD= 25m)时,能够安全起吊重物的最大质量是多少?
(2)当OE= 15m时,用此塔吊将0.8t的钢材先竖直匀速吊起8m,然后沿水平方向缓缓移动4m,送达指定位置。在这一过程中,塔吊对钢材做了多少功?

答案:(1)m_max=0.48t (2)6.4×10⁴J
解析:
(1)由杠杆平衡条件可得:$m_{配重}g \cdot OC = m_1g \cdot OE$,$m_{配重}g \cdot OC = m_{max}g \cdot OD$。
则$m_1 \cdot OE = m_{max} \cdot OD$,$m_{max} = \frac{m_1 \cdot OE}{OD} = \frac{0.8\,t × 15\,m}{25\,m} = 0.48\,t$。
(2)钢材重力$G = mg = 0.8 × 10^3\,kg × 10\,N/kg = 8 × 10^3\,N$。
竖直吊起做功$W = Gh = 8 × 10^3\,N × 8\,m = 6.4 × 10^4\,J$,水平移动不做功,总功为$6.4 × 10^4\,J$。
则$m_1 \cdot OE = m_{max} \cdot OD$,$m_{max} = \frac{m_1 \cdot OE}{OD} = \frac{0.8\,t × 15\,m}{25\,m} = 0.48\,t$。
(2)钢材重力$G = mg = 0.8 × 10^3\,kg × 10\,N/kg = 8 × 10^3\,N$。
竖直吊起做功$W = Gh = 8 × 10^3\,N × 8\,m = 6.4 × 10^4\,J$,水平移动不做功,总功为$6.4 × 10^4\,J$。