7. 如图甲所示,电源电压保持不变,小灯泡的额定电压为$12\ V$。闭合开关$S$后,当滑片$P$从最右端滑到最左端的过程中,小灯泡的$I-U$关系图像如图乙所示,则小灯泡的额定功率为

24
W,电源电压为12
V,滑动变阻器的最大阻值为9
Ω。
答案:7. 24 12 9
解析:
解:
1. 小灯泡的额定功率:
小灯泡额定电压为 $ U_{额} = 12\ V $,由图乙知此时电流 $ I_{额} = 2.0\ A $,
额定功率 $ P_{额} = U_{额} I_{额} = 12\ V × 2.0\ A = 24\ W $。
2. 电源电压:
当滑片在最左端时,滑动变阻器接入电阻为 $ 0 $,电路中只有灯泡,此时灯泡电压等于电源电压。由图乙知,此时灯泡电压为 $ 12\ V $,故电源电压 $ U = 12\ V $。
3. 滑动变阻器的最大阻值:
当滑片在最右端时,滑动变阻器接入最大阻值 $ R_{max} $,此时电路电流最小。由图乙知,此时灯泡电压 $ U_L = 3\ V $,电流 $ I = 1.0\ A $,
滑动变阻器两端电压 $ U_R = U - U_L = 12\ V - 3\ V = 9\ V $,
最大阻值 $ R_{max} = \frac{U_R}{I} = \frac{9\ V}{1.0\ A} = 9\ \Omega $。
答案:24;12;9。
1. 小灯泡的额定功率:
小灯泡额定电压为 $ U_{额} = 12\ V $,由图乙知此时电流 $ I_{额} = 2.0\ A $,
额定功率 $ P_{额} = U_{额} I_{额} = 12\ V × 2.0\ A = 24\ W $。
2. 电源电压:
当滑片在最左端时,滑动变阻器接入电阻为 $ 0 $,电路中只有灯泡,此时灯泡电压等于电源电压。由图乙知,此时灯泡电压为 $ 12\ V $,故电源电压 $ U = 12\ V $。
3. 滑动变阻器的最大阻值:
当滑片在最右端时,滑动变阻器接入最大阻值 $ R_{max} $,此时电路电流最小。由图乙知,此时灯泡电压 $ U_L = 3\ V $,电流 $ I = 1.0\ A $,
滑动变阻器两端电压 $ U_R = U - U_L = 12\ V - 3\ V = 9\ V $,
最大阻值 $ R_{max} = \frac{U_R}{I} = \frac{9\ V}{1.0\ A} = 9\ \Omega $。
答案:24;12;9。
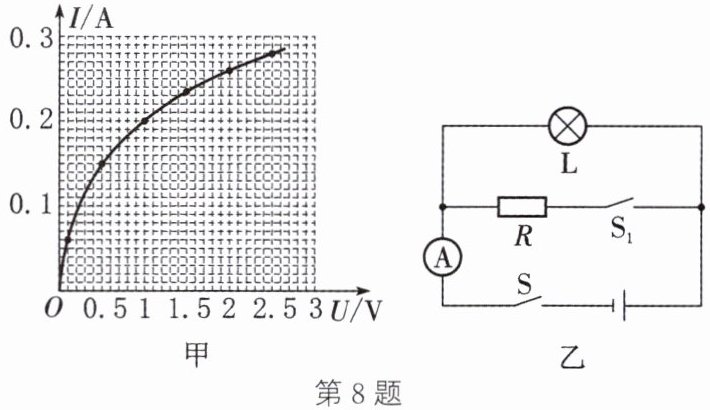
8. 图甲是通过小灯泡$L$的电流$I$随其两端电压$U$变化的图像。将小灯泡$L$和定值电阻$R$接入如图乙所示的电路中,只闭合开关$S$时,小灯泡的实际功率为$0.7\ W$。开关$S$、$S_1$都闭合时,电流表的示数为$0.48\ A$。已知电源两端电压保持不变,下列说法中正确的是
(
A.由图甲可知小灯泡的阻值不变
B.电源电压为$5\ V$
C.电阻$R$的阻值为$12.5\ \Omega$
D.电路消耗的最大总功率为$2.88\ W$
(
C
)
A.由图甲可知小灯泡的阻值不变
B.电源电压为$5\ V$
C.电阻$R$的阻值为$12.5\ \Omega$
D.电路消耗的最大总功率为$2.88\ W$
答案:8. C
解析:
解:
A选项:由图甲,$I-U$图像为曲线,$R=\frac{U}{I}$变化,A错误。
B选项:只闭合$S$时,灯$L$单独工作,$P=UI=0.7\ W$。查图甲,$U=2.5\ V$、$I=0.28\ A$时,$UI=2.5\ V×0.28\ A=0.7\ W$,故电源电压$U=2.5\ V$,B错误。
C选项:$S$、$S_1$闭合时,$L$与$R$并联,电流表测总电流$I_{总}=0.48\ A$。此时灯$L$电压仍为$2.5\ V$,由图甲得$I_L=0.28\ A$。通过$R$的电流$I_R=I_{总}-I_L=0.48\ A-0.28\ A=0.2\ A$。$R=\frac{U}{I_R}=\frac{2.5\ V}{0.2\ A}=12.5\ \Omega$,C正确。
D选项:电路最大总功率在$S$、$S_1$闭合时,$P_{总}=UI_{总}=2.5\ V×0.48\ A=1.2\ W$,D错误。
答案:C
A选项:由图甲,$I-U$图像为曲线,$R=\frac{U}{I}$变化,A错误。
B选项:只闭合$S$时,灯$L$单独工作,$P=UI=0.7\ W$。查图甲,$U=2.5\ V$、$I=0.28\ A$时,$UI=2.5\ V×0.28\ A=0.7\ W$,故电源电压$U=2.5\ V$,B错误。
C选项:$S$、$S_1$闭合时,$L$与$R$并联,电流表测总电流$I_{总}=0.48\ A$。此时灯$L$电压仍为$2.5\ V$,由图甲得$I_L=0.28\ A$。通过$R$的电流$I_R=I_{总}-I_L=0.48\ A-0.28\ A=0.2\ A$。$R=\frac{U}{I_R}=\frac{2.5\ V}{0.2\ A}=12.5\ \Omega$,C正确。
D选项:电路最大总功率在$S$、$S_1$闭合时,$P_{总}=UI_{总}=2.5\ V×0.48\ A=1.2\ W$,D错误。
答案:C
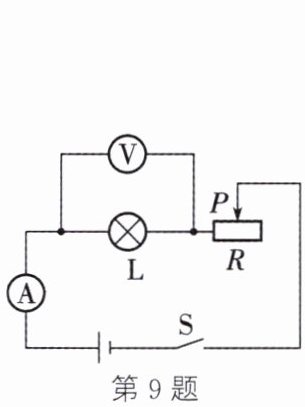
9. 某同学在做“调节灯泡亮度”的电学实验时,电路如图所示。电源电压恒为$6\ V$,电流表的量程为“$0∼0.6\ A$”,电压表的量程为“$0∼3\ V$”,滑动变阻器的规格为“$20\ \Omega\ \ 2\ A$”,灯泡$L$标有“$3\ V\ \ 0.9\ W$”字样(忽略灯丝电阻变化)。在实验中为了保证所有元件的安全,下列判断正确的是
(
A.该电路中,变阻器$R$接入电路的阻值变化范围是$0∼20\ \Omega$
B.该电路中,电流表示数的变化范围是$0.2∼0.6\ A$
C.该电路中,电压表示数的变化范围是$2∼3\ V$
D.该电路中,灯泡消耗功率的变化范围是$0.4∼3.6\ W$
(
C
)
A.该电路中,变阻器$R$接入电路的阻值变化范围是$0∼20\ \Omega$
B.该电路中,电流表示数的变化范围是$0.2∼0.6\ A$
C.该电路中,电压表示数的变化范围是$2∼3\ V$
D.该电路中,灯泡消耗功率的变化范围是$0.4∼3.6\ W$
答案:9. C
解析:
解:
1. 灯泡电阻:$R_{L}=\frac{U_{L}^{2}}{P_{L}}=\frac{(3\ V)^{2}}{0.9\ W}=10\ \Omega$
2. 电路最大电流(灯泡正常发光时):$I_{max}=\frac{P_{L}}{U_{L}}=\frac{0.9\ W}{3\ V}=0.3\ A$(小于电流表量程0.6A和变阻器允许电流2A)
3. 滑动变阻器最小阻值:$R_{min}=\frac{U-U_{L}}{I_{max}}=\frac{6\ V-3\ V}{0.3\ A}=10\ \Omega$
4. 滑动变阻器最大阻值时电路电流:$I_{min}=\frac{U}{R_{L}+R_{max}}=\frac{6\ V}{10\ \Omega+20\ \Omega}=0.2\ A$
5. 电压表示数范围:
最大:$U_{Vmax}=3\ V$(灯泡额定电压)
最小:$U_{Vmin}=I_{min}R_{L}=0.2\ A×10\ \Omega=2\ V$,即$2\ V \sim 3\ V$
6. 结论:电压表示数变化范围为$2\ V \sim 3\ V$
C
1. 灯泡电阻:$R_{L}=\frac{U_{L}^{2}}{P_{L}}=\frac{(3\ V)^{2}}{0.9\ W}=10\ \Omega$
2. 电路最大电流(灯泡正常发光时):$I_{max}=\frac{P_{L}}{U_{L}}=\frac{0.9\ W}{3\ V}=0.3\ A$(小于电流表量程0.6A和变阻器允许电流2A)
3. 滑动变阻器最小阻值:$R_{min}=\frac{U-U_{L}}{I_{max}}=\frac{6\ V-3\ V}{0.3\ A}=10\ \Omega$
4. 滑动变阻器最大阻值时电路电流:$I_{min}=\frac{U}{R_{L}+R_{max}}=\frac{6\ V}{10\ \Omega+20\ \Omega}=0.2\ A$
5. 电压表示数范围:
最大:$U_{Vmax}=3\ V$(灯泡额定电压)
最小:$U_{Vmin}=I_{min}R_{L}=0.2\ A×10\ \Omega=2\ V$,即$2\ V \sim 3\ V$
6. 结论:电压表示数变化范围为$2\ V \sim 3\ V$
C
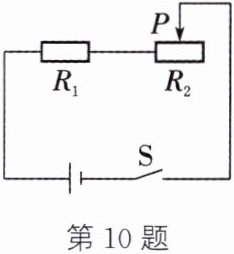
10. ($2025·$徐州沛县一模)如图所示电路,电源电压保持$9\ V$不变,$R_1$是定值电阻,$R_2$是最大阻值为$60\ \Omega$的滑动变阻器。闭合开关,当$R_2$的滑片位于最左端时,电路中的电流为$0.6\ A$。求:
(1) 电阻$R_1$的阻值。
(2) 滑片从最左端移动到最右端的过程中,滑动变阻器的最大功率。
(1) 电阻$R_1$的阻值。
(2) 滑片从最左端移动到最右端的过程中,滑动变阻器的最大功率。

答案:10. (1) 闭合开关,当$R_2$的滑片位于最左端时,电路中只有$R_1$接入电路,则电阻$R_1$的阻值$R_1 = \frac{U}{I} = \frac{9V}{0.6A} = 15\Omega$ (2) 滑片从最左端移动到最右端的过程中,滑动变阻器的功率$P_2 = (\frac{U}{R_1 + R_2})^2R_2 = \frac{U^2R_2}{(R_1 - R_2)^2 + 4R_1R_2}$,当$R_1 = R_2 = 15\Omega$时,滑动变阻器的功率最大,即最大功率$P_2 = \frac{U^2}{4R_1} = \frac{(9V)^2}{4 × 15\Omega} = 1.35W$
解析:
(1) 解:当$R_2$的滑片位于最左端时,电路中只有$R_1$接入电路,由$I = \frac{U}{R}$可得,$R_1=\frac{U}{I}=\frac{9\ V}{0.6\ A} = 15\ \Omega$
(2) 解:滑动变阻器的功率$P_2=\left(\frac{U}{R_1 + R_2}\right)^2R_2=\frac{U^2R_2}{(R_1 + R_2)^2}$,当$R_2 = R_1 = 15\ \Omega$时,$P_2$最大,$P_{2max}=\frac{U^2}{4R_1}=\frac{(9\ V)^2}{4×15\ \Omega}=1.35\ W$
(2) 解:滑动变阻器的功率$P_2=\left(\frac{U}{R_1 + R_2}\right)^2R_2=\frac{U^2R_2}{(R_1 + R_2)^2}$,当$R_2 = R_1 = 15\ \Omega$时,$P_2$最大,$P_{2max}=\frac{U^2}{4R_1}=\frac{(9\ V)^2}{4×15\ \Omega}=1.35\ W$