8. 在如图所示的电路中,电源电压为$6\ V$,电阻$R_1$为$10\ \Omega$。闭合开关$S$后,电流表的示数为$0.2\ A$,电源电压保持不变。求:
(1)$R_1$在$10\ s$内所消耗的电能$W_1$。
(2)$R_2$消耗$16\ J$的电能所需的时间。

(1)$R_1$在$10\ s$内所消耗的电能$W_1$。
(2)$R_2$消耗$16\ J$的电能所需的时间。

答案:8. (1)由图可知,R₁、R₂串联,串联电路电流处处相等,所以 I₁ = I₂ = 0.2 A,R₁在10 s内所消耗的电能W₁ = I₁²R₁t₁ = (0.2 A)² × 10 Ω × 10 s = 4 J (2)由$ I = \frac{U}{R}$可得R₁两端的电压U₁ = I₁R₁ = 0.2 A × 10 Ω = 2 V;串联电路的总电压等于各部分电路的电压之和,R₂两端的电压U₂ = U - U₁ = 6 V - 2 V = 4 V,由W = UIt可得R₂消耗16 J的电能所需的时间$t₂ = \frac{W₂}{U₂I₂} = \frac{16 J}{4 V × 0.2 A} = 20 s$
解析:
解:(1)由图可知,$R_1$、$R_2$串联,串联电路电流处处相等,所以$I_1 = I_2 = 0.2\ A$。
$R_1$在$10\ s$内所消耗的电能:
$W_1 = I_1^2 R_1 t_1 = (0.2\ A)^2 × 10\ \Omega × 10\ s = 4\ J$
(2)由$I = \frac{U}{R}$可得$R_1$两端的电压:
$U_1 = I_1 R_1 = 0.2\ A × 10\ \Omega = 2\ V$
串联电路总电压等于各部分电路电压之和,$R_2$两端的电压:
$U_2 = U - U_1 = 6\ V - 2\ V = 4\ V$
由$W = UIt$可得$R_2$消耗$16\ J$电能所需的时间:
$t_2 = \frac{W_2}{U_2 I_2} = \frac{16\ J}{4\ V × 0.2\ A} = 20\ s$
(1)$4\ J$;(2)$20\ s$
$R_1$在$10\ s$内所消耗的电能:
$W_1 = I_1^2 R_1 t_1 = (0.2\ A)^2 × 10\ \Omega × 10\ s = 4\ J$
(2)由$I = \frac{U}{R}$可得$R_1$两端的电压:
$U_1 = I_1 R_1 = 0.2\ A × 10\ \Omega = 2\ V$
串联电路总电压等于各部分电路电压之和,$R_2$两端的电压:
$U_2 = U - U_1 = 6\ V - 2\ V = 4\ V$
由$W = UIt$可得$R_2$消耗$16\ J$电能所需的时间:
$t_2 = \frac{W_2}{U_2 I_2} = \frac{16\ J}{4\ V × 0.2\ A} = 20\ s$
(1)$4\ J$;(2)$20\ s$
9. 甲、乙两灯的电流随电压变化的关系图像如图所示。若将甲、乙两灯并联接入$4\ V$的电路中,则两灯在$5\ min$内消耗的总电能为

960
$J$;若将甲、乙两灯串联接入$9\ V$的电路中,则通电$10\ s$两灯消耗的总电能为36
$J$。
答案:9. 960 36
解析:
解:
1. 并联接入4V电路:
由图像知,$U=4V$时,$I_{甲}=0.5A$,$I_{乙}=0.3A$
总电流$I=I_{甲}+I_{乙}=0.5A + 0.3A=0.8A$
时间$t=5min=300s$
总电能$W=UIt=4V×0.8A×300s=960J$
2. 串联接入9V电路:
串联电路电流相等,由图像知,当$I=0.4A$时,$U_{甲}=5V$,$U_{乙}=4V$,$U_{甲}+U_{乙}=9V$
总电能$W=UIt=9V×0.4A×10s=36J$
960;36
1. 并联接入4V电路:
由图像知,$U=4V$时,$I_{甲}=0.5A$,$I_{乙}=0.3A$
总电流$I=I_{甲}+I_{乙}=0.5A + 0.3A=0.8A$
时间$t=5min=300s$
总电能$W=UIt=4V×0.8A×300s=960J$
2. 串联接入9V电路:
串联电路电流相等,由图像知,当$I=0.4A$时,$U_{甲}=5V$,$U_{乙}=4V$,$U_{甲}+U_{乙}=9V$
总电能$W=UIt=9V×0.4A×10s=36J$
960;36
10. 一电阻丝通过的电流为$I$,在$t$时间内消耗的电能是$W$。如果通过它的电流增加到$3I$,那么在相同时间内消耗的电能是
(
A.$3W$
B.$6W$
C.$9W$
D.$18W$
(
C
)A.$3W$
B.$6W$
C.$9W$
D.$18W$
答案:10. C
解析:
根据电能公式$W=I^{2}Rt$,当电流为$I$时,$W=I^{2}Rt$。电流增加到$3I$,时间仍为$t$,电阻$R$不变,此时电能$W'=(3I)^{2}Rt = 9I^{2}Rt = 9W$。
C
C
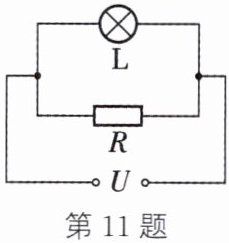
11. 如图所示,灯泡$L$和电阻并联后接在电压为$U$的电路中,已知电阻的阻值为$R$,通过电路的总电流为$I$,则灯泡$L$在$t$时间内消耗的电能是
(
A.$UIt$
B.$\frac{U^2}{R}t$
C.$I^2Rt$
D.$UIt - \frac{U^2}{R}t$
(
D
)
A.$UIt$
B.$\frac{U^2}{R}t$
C.$I^2Rt$
D.$UIt - \frac{U^2}{R}t$
答案:11. D
解析:
解:灯泡$L$和电阻$R$并联,电源电压为$U$,总电流为$I$。
电路总电能$W_{总}=UIt$。
电阻$R$消耗的电能$W_{R}=\frac{U^{2}}{R}t$。
灯泡$L$消耗的电能$W_{L}=W_{总} - W_{R}=UIt-\frac{U^{2}}{R}t$。
答案:D
电路总电能$W_{总}=UIt$。
电阻$R$消耗的电能$W_{R}=\frac{U^{2}}{R}t$。
灯泡$L$消耗的电能$W_{L}=W_{总} - W_{R}=UIt-\frac{U^{2}}{R}t$。
答案:D
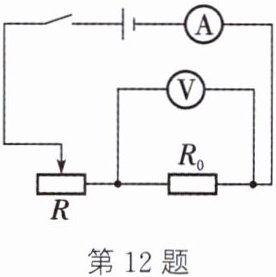
12. 如图,电源电压为$6\ V$,电阻$R_0 = 10\ \Omega$,电流表量程为$0\sim0.6\ A$,电压表量程为$0\sim3\ V$,滑动变阻器$R$上标有“$20\ \Omega\ \ 0.5\ A$”字样。求:
(1)当电路中电流最小时,$2\ min$内电流通过电阻$R_0$做的功。
(2)当电路中电流最大时,$2\ min$整个电路消耗的电能。
(1)当电路中电流最小时,$2\ min$内电流通过电阻$R_0$做的功。
(2)当电路中电流最大时,$2\ min$整个电路消耗的电能。

答案:12. (1)当滑动变阻器接入电路中的电阻最大时,电路中的电流最小,电路中的电流$I = \frac{U}{R + R₀} = \frac{6 V}{20 Ω + 10 Ω} = 0.2 A,$则2 min内电流通过电阻R₀做的功W₀ = I²R₀t = (0.2 A)² × 10 Ω × 2 × 60 s = 48 J (2)当电压表的示数U₀ = 3 V时,通过R₀的电流$I₀ = \frac{U₀}{R₀} = \frac{3 V}{10 Ω} = 0.3 A,$因电流表的量程为0~0.6 A,滑动变阻器允许通过的最大电流为0.5 A,则电路中的最大电流为0.3 A,2 min整个电路消耗的电能W = UI₀t' = 6 V × 0.3 A × 2 × 60 s = 216 J
解析:
(1)当滑动变阻器接入电路中的电阻最大时,电路中的电流最小,电路中的电流$I = \frac{U}{R + R_0} = \frac{6\ V}{20\ \Omega + 10\ \Omega} = 0.2\ A$,则$2\ min$内电流通过电阻$R_0$做的功$W_0 = I^2R_0t = (0.2\ A)^2 × 10\ \Omega × 2 × 60\ s = 48\ J$。
(2)当电压表的示数$U_0 = 3\ V$时,通过$R_0$的电流$I_0 = \frac{U_0}{R_0} = \frac{3\ V}{10\ \Omega} = 0.3\ A$,因电流表的量程为$0\sim0.6\ A$,滑动变阻器允许通过的最大电流为$0.5\ A$,则电路中的最大电流为$0.3\ A$,$2\ min$整个电路消耗的电能$W = UI_0t' = 6\ V × 0.3\ A × 2 × 60\ s = 216\ J$。
(2)当电压表的示数$U_0 = 3\ V$时,通过$R_0$的电流$I_0 = \frac{U_0}{R_0} = \frac{3\ V}{10\ \Omega} = 0.3\ A$,因电流表的量程为$0\sim0.6\ A$,滑动变阻器允许通过的最大电流为$0.5\ A$,则电路中的最大电流为$0.3\ A$,$2\ min$整个电路消耗的电能$W = UI_0t' = 6\ V × 0.3\ A × 2 × 60\ s = 216\ J$。
13. (新情境·日常生活)某电动自行车的蓄电池标有“$36\ V\ \ 10\ A·h$”的字样,若该车以$10\ m/s$的速度匀速沿平直公路行驶,受到的阻力为$20\ N$,电能转化为机械能的效率为$75\%$,则该车充一次电后,以所述情况行驶时,最多能行驶
48.6
$km$。答案:13. 48.6
解析:
蓄电池储存的电能:$W_{电}=UIt=36\ V × 10\ A·h=36\ V × 10\ A × 3600\ s=1.296 × 10^{6}\ J$
转化的机械能:$W_{机}=W_{电} × \eta=1.296 × 10^{6}\ J × 75\%=9.72 × 10^{5}\ J$
因车匀速行驶,牵引力$F=f=20\ N$
行驶距离:$s=\frac{W_{机}}{F}=\frac{9.72 × 10^{5}\ J}{20\ N}=4.86 × 10^{4}\ m=48.6\ km$
转化的机械能:$W_{机}=W_{电} × \eta=1.296 × 10^{6}\ J × 75\%=9.72 × 10^{5}\ J$
因车匀速行驶,牵引力$F=f=20\ N$
行驶距离:$s=\frac{W_{机}}{F}=\frac{9.72 × 10^{5}\ J}{20\ N}=4.86 × 10^{4}\ m=48.6\ km$