活动一:概念回顾
1. 我们学习了频数和频率,它们的区别和联系是什么?
2. 如果事件发生的各种结果的可能性相同,结果总数为 $n$,事件 $A$ 发生的可能的结果总数为 $m$,那么事件 $A$ 发生的概率$P(A)=$
1. 我们学习了频数和频率,它们的区别和联系是什么?
2. 如果事件发生的各种结果的可能性相同,结果总数为 $n$,事件 $A$ 发生的可能的结果总数为 $m$,那么事件 $A$ 发生的概率$P(A)=$
$\frac{m}{n}$
.答案:解:频数是指在试验当中,事件发生的次数;频率是指在试验当中,该事件发生次数比上总次数的值。
$\frac {m}{n}$
$\frac {m}{n}$
活动二:典例评析
1. 某市体育中考现场考试内容有三项:$50 m$ 跑为必测项目,立定跳远、实心球中任选一项,坐位体前屈、$1 min$ 跳绳中任选一项.
(1)每位考生有
(2)用画树状图或列表的方法求小明与小刚选择同种方案的概率(各种方案用 $A、B、C·s$或①、②、③$·s$符号来代表以简化解答过程).
2.【研究问题】 一只不透明的盒中装有若干个除颜色外都相同的红球和黄球.采用下面的方法估算不同颜色球的数量.
【操作方法】 先从盒中摸出 $8$ 个球,画上记号放回盒中,再进行摸球试验(摸球试验的要求:先搅拌均匀,每次摸出 $1$ 个球,放回盒中后再继续).
【活动结果】 摸球试验活动一共做了 $50$ 次,统计结果如下表:

(1)估计盒中红球、黄球占总球数的百分比分别是多少.
(2)估计盒中红球有多少个.
1. 某市体育中考现场考试内容有三项:$50 m$ 跑为必测项目,立定跳远、实心球中任选一项,坐位体前屈、$1 min$ 跳绳中任选一项.
(1)每位考生有
4
种选择方案;(2)用画树状图或列表的方法求小明与小刚选择同种方案的概率(各种方案用 $A、B、C·s$或①、②、③$·s$符号来代表以简化解答过程).
2.【研究问题】 一只不透明的盒中装有若干个除颜色外都相同的红球和黄球.采用下面的方法估算不同颜色球的数量.
【操作方法】 先从盒中摸出 $8$ 个球,画上记号放回盒中,再进行摸球试验(摸球试验的要求:先搅拌均匀,每次摸出 $1$ 个球,放回盒中后再继续).
【活动结果】 摸球试验活动一共做了 $50$ 次,统计结果如下表:

(1)估计盒中红球、黄球占总球数的百分比分别是多少.
(2)估计盒中红球有多少个.
答案:
4
解: (2)把4种方案分别列为:A:立定跳远、坐位体前屈; B:实心球,$1 \mathrm {\ \mathrm {min}}$跳绳;
C:立定跳远、$1 \mathrm {\ \mathrm {min}}$跳绳;D:实心球,坐位体前屈
画树状图如下
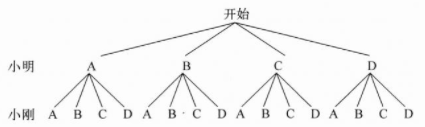
∴小明与小刚选择同种方案的概率$=\frac {4}{16}=\frac {1}{4}$
解: (1)由题意可知: 50次摸球活动中,出现红球20次,黄球30次
∴红球所占百分比为20÷50=40\%,黄球所占百分比为30÷50= 60\%
∴红球占40\%,黄球占60\%
(2)由题意可知,50次摸球活动中,出现有记号的球4次
∴总球数为$\frac {50}{4}×8= 100$
∴红球数为100×40\%=40
4
解: (2)把4种方案分别列为:A:立定跳远、坐位体前屈; B:实心球,$1 \mathrm {\ \mathrm {min}}$跳绳;
C:立定跳远、$1 \mathrm {\ \mathrm {min}}$跳绳;D:实心球,坐位体前屈
画树状图如下

∴小明与小刚选择同种方案的概率$=\frac {4}{16}=\frac {1}{4}$
解: (1)由题意可知: 50次摸球活动中,出现红球20次,黄球30次
∴红球所占百分比为20÷50=40\%,黄球所占百分比为30÷50= 60\%
∴红球占40\%,黄球占60\%
(2)由题意可知,50次摸球活动中,出现有记号的球4次
∴总球数为$\frac {50}{4}×8= 100$
∴红球数为100×40\%=40