1. 在$\triangle ABC$中,$\angle B = 90^{\circ}$,$BC = 2AB$,则$\tan A =$
2
.答案:2
2. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD \perp AB$,垂足为$D$,$CD = 3$,$AD = 4$,则$\tan A =$

$\frac{3}{4}$
,$\tan B =$$\frac{4}{3}$
.
答案:$\frac {3}{4}$
$\frac {4}{3}$
$\frac {4}{3}$
3. 如图是一块三角尺,$AC = 30\ cm$,$\angle C = 90^{\circ}$,$\tan\angle BAC = \frac{\sqrt{3}}{3}$,则$BC$的长为

10$\sqrt{3}$
$cm$.
答案:$10\sqrt 3$
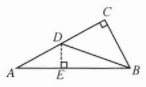
4. 如图,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$BC = \sqrt{5}$,点$D$在$AC$上,连接$BD$. 若$\tan A = \frac{1}{2}$,$\tan\angle ABD = \frac{1}{3}$,求$CD$的长.


答案:
解:在Rt△ABC中,∠C=90°,$BC=\sqrt{5}$
∴$ tan A=\frac {BC}{AC} =\frac {1}{2}$
∴$AC=2BC=2\ \mathrm {AB}= 2 \sqrt{5} $
由勾股定理,得$AB=\sqrt{AC^2+BC^2}=5$
过点D作DE⊥AB,垂足为E,如图所示
∵$ tan ∠ABD=\frac {DE}{BE}=\frac {1}{3}$
∴ BE=3DE
∵$ tan A=\frac {DE}{AE}=\frac {1}{2}$
∴ AE=2DE
∵ AB=BE+AE=5DE=5
∴ DE=1,AE=2
由勾股定理,得$AD=\sqrt{5} $
\
∴$ CD=AC-AD=\sqrt{5}$
解:在Rt△ABC中,∠C=90°,$BC=\sqrt{5}$
∴$ tan A=\frac {BC}{AC} =\frac {1}{2}$
∴$AC=2BC=2\ \mathrm {AB}= 2 \sqrt{5} $
由勾股定理,得$AB=\sqrt{AC^2+BC^2}=5$
过点D作DE⊥AB,垂足为E,如图所示
∵$ tan ∠ABD=\frac {DE}{BE}=\frac {1}{3}$
∴ BE=3DE
∵$ tan A=\frac {DE}{AE}=\frac {1}{2}$
∴ AE=2DE
∵ AB=BE+AE=5DE=5
∴ DE=1,AE=2
由勾股定理,得$AD=\sqrt{5} $
\
∴$ CD=AC-AD=\sqrt{5}$

1. 在平面直角坐标系中,$\triangle ABC$的三个顶点的坐标分别为$A(-4,1)$、$B(-1,3)$、$C(-4,3)$,求$\tan B$的值.
答案:解:∵点A与点C的横坐标相同,点B与点C的纵坐标相同
∴∠ACB=90°
∵AC=2,BC=3
∴$tanB =\frac {AC}{BC}=\frac {2}{3}$
∴∠ACB=90°
∵AC=2,BC=3
∴$tanB =\frac {AC}{BC}=\frac {2}{3}$
2. 如图,$\triangle ABC$的顶点是正方形网格的格点,则$\tan A$的值为(

A.$\frac{1}{2}$
B.$\frac{\sqrt{5}}{5}$
C.$\frac{\sqrt{10}}{10}$
D.$\frac{2\sqrt{5}}{5}$
A
).
A.$\frac{1}{2}$
B.$\frac{\sqrt{5}}{5}$
C.$\frac{\sqrt{10}}{10}$
D.$\frac{2\sqrt{5}}{5}$
答案:A
3. 小明在学习“锐角三角函数”时发现:将如图所示的矩形纸片$ABCD$沿过点$B$的直线折叠,使点$A$落在$BC$的点$E$处;还原后,再沿过点$E$的直线折叠,使点$A$落在$BC$的点$F$处,这样就可以求出$67.5^{\circ}$角的正切值,则$\tan 67.5^{\circ}$的值为

$\sqrt{2}+1$
.
答案:$\sqrt 2+1$