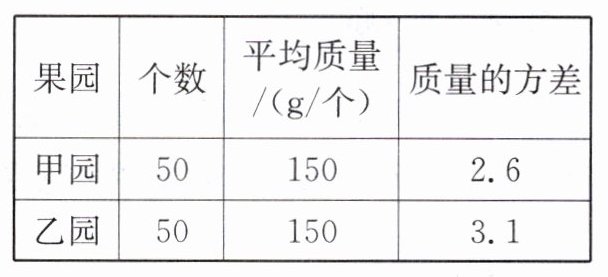
1. 某公司要购进一批规格为 150 g/个的苹果,现有两个果园提供货源.质检员分别从甲、乙两园的产品中随机抽取了 50 个苹果称重,并将所得数据处理后制成右表.下列说法中,错误的是(
A.本次调查方式是抽样调查
B.甲、乙两园被抽取苹果的平均质量相同
C.被抽取的这 100 个苹果的质量是本次调查的样本
D.甲园苹果的质量比乙园苹果的质量波动大
D
).
A.本次调查方式是抽样调查
B.甲、乙两园被抽取苹果的平均质量相同
C.被抽取的这 100 个苹果的质量是本次调查的样本
D.甲园苹果的质量比乙园苹果的质量波动大
答案:D
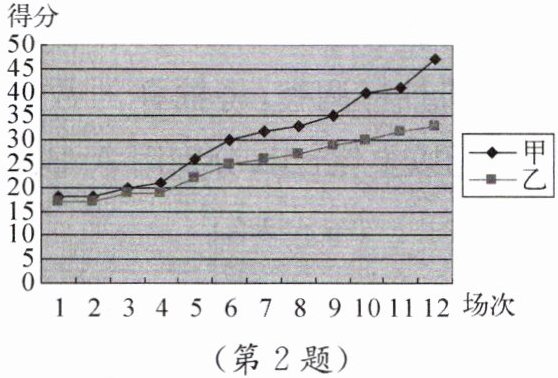
2. 甲、乙两名篮球运动员某赛季 12 场比赛得分情况如图所示,对这两名运动员的成绩进行比较.下列四个结论中,不正确的是(
A.甲得分的极差大于乙得分的极差
B.甲得分的中位数大于乙得分的中位数
C.甲得分的平均数大于乙得分的平均数
D.甲的成绩比乙的成绩稳定
D
).
A.甲得分的极差大于乙得分的极差
B.甲得分的中位数大于乙得分的中位数
C.甲得分的平均数大于乙得分的平均数
D.甲的成绩比乙的成绩稳定
答案:D
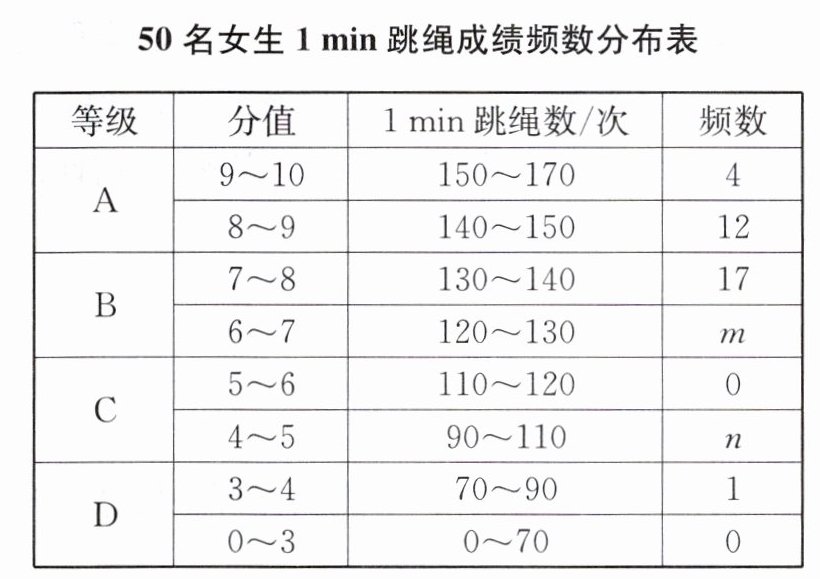
某校九年级共有 50 名女生选考 1min 跳绳,根据测试评分标准,将她们的成绩进行统计后分为 A、B、C、D 四个等级,并绘制了下面的扇形统计图和频数分布表(6~7 的意义为大于等于 6 分且小于 7 分,其余类似).

(1)A 等级人数的百分比是
(2)求$m、n$的值.
(3)在抽取的这个样本中,哪个分数段的学生最多?请你帮助老师计算这次 1 min 跳绳测试的及格率[6 分以上(含 6 分)为及格].


(1)A 等级人数的百分比是
32%
.(2)求$m、n$的值.
(3)在抽取的这个样本中,哪个分数段的学生最多?请你帮助老师计算这次 1 min 跳绳测试的及格率[6 分以上(含 6 分)为及格].
答案:32%
解: (2)根据题意,得m+n= 50-(4+12+17+1)=16
$\frac {17+m}{50}×100\%=64\%$
$\begin{cases}{m+n=16 } \\{17+m=32} \end{cases} $解得$\begin{cases}{m=15}\\{n=1}\end{cases}$
(3)7∽8分数段的学生最多,
及格人数=4+12+17+15=48(人),
及格率$=\frac {48}{50}×100\%=96\%$
答:这次测试的及格率为96\%。
解: (2)根据题意,得m+n= 50-(4+12+17+1)=16
$\frac {17+m}{50}×100\%=64\%$
$\begin{cases}{m+n=16 } \\{17+m=32} \end{cases} $解得$\begin{cases}{m=15}\\{n=1}\end{cases}$
(3)7∽8分数段的学生最多,
及格人数=4+12+17+15=48(人),
及格率$=\frac {48}{50}×100\%=96\%$
答:这次测试的及格率为96\%。