15. (7 分)如图(2)是由几个完全相同的小正方体搭成的一个几何体,每个小正方体的棱长为 $ 1cm $.

(1)请画出从不同方向看该几何体得到的平面图形;(在图(1)所提供的方格内画上即可)

(2)如果小明还想添加一些相同的小正方体,并保持从上面和左面看到的形状图不变,最多可以再添加
(3)请计算出图(2)几何体的表面积(包括与地面接触的部分).

(1)请画出从不同方向看该几何体得到的平面图形;(在图(1)所提供的方格内画上即可)

(2)如果小明还想添加一些相同的小正方体,并保持从上面和左面看到的形状图不变,最多可以再添加
7
个小正方体;(3)请计算出图(2)几何体的表面积(包括与地面接触的部分).
答案:
15. (1)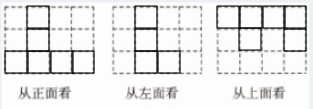
;(2) 7;(3) 36 cm².
15. (1)

;(2) 7;(3) 36 cm².
16. (10 分)如图,花丛中有一路灯杆 $ AB $,在灯光下,大华在 $ D $ 处的影长 $ DE = 3m $,沿 $ BD $ 方向行走到达 $ G $ 点,$ DG = 5m $,这时大华的影长 $ GH = 5m $. 如果大华的身高为 $ 2m $,求路灯杆 $ AB $ 的高度.


答案:16. 路灯杆AB的高度为7 m.
解析:
解:设路灯杆$AB$的高度为$h\ \mathrm{m}$,$BD = x\ \mathrm{m}$。
因为大华身高为$2\ \mathrm{m}$,在$D$处影长$DE = 3\ \mathrm{m}$,所以$BE=BD + DE=(x + 3)\ \mathrm{m}$。
由于$CD⊥ BH$,$AB⊥ BH$,则$CD// AB$,$△ CDE∼△ ABE$,可得$\frac{CD}{AB}=\frac{DE}{BE}$,即$\frac{2}{h}=\frac{3}{x + 3}$,整理得$3h = 2(x + 3)$,即$3h=2x + 6$ ①。
大华沿$BD$方向行走$DG = 5\ \mathrm{m}$到达$G$点,此时$BG=BD + DG=(x + 5)\ \mathrm{m}$,影长$GH = 5\ \mathrm{m}$,所以$BH=BG + GH=(x + 5 + 5)=(x + 10)\ \mathrm{m}$。
同理,$FG⊥ BH$,$AB⊥ BH$,则$FG// AB$,$△ FGH∼△ ABH$,可得$\frac{FG}{AB}=\frac{GH}{BH}$,即$\frac{2}{h}=\frac{5}{x + 10}$,整理得$5h = 2(x + 10)$,即$5h=2x + 20$ ②。
② - ①得:$5h-3h=2x + 20-(2x + 6)$,$2h = 14$,解得$h = 7$。
路灯杆$AB$的高度为$7\ \mathrm{m}$。
因为大华身高为$2\ \mathrm{m}$,在$D$处影长$DE = 3\ \mathrm{m}$,所以$BE=BD + DE=(x + 3)\ \mathrm{m}$。
由于$CD⊥ BH$,$AB⊥ BH$,则$CD// AB$,$△ CDE∼△ ABE$,可得$\frac{CD}{AB}=\frac{DE}{BE}$,即$\frac{2}{h}=\frac{3}{x + 3}$,整理得$3h = 2(x + 3)$,即$3h=2x + 6$ ①。
大华沿$BD$方向行走$DG = 5\ \mathrm{m}$到达$G$点,此时$BG=BD + DG=(x + 5)\ \mathrm{m}$,影长$GH = 5\ \mathrm{m}$,所以$BH=BG + GH=(x + 5 + 5)=(x + 10)\ \mathrm{m}$。
同理,$FG⊥ BH$,$AB⊥ BH$,则$FG// AB$,$△ FGH∼△ ABH$,可得$\frac{FG}{AB}=\frac{GH}{BH}$,即$\frac{2}{h}=\frac{5}{x + 10}$,整理得$5h = 2(x + 10)$,即$5h=2x + 20$ ②。
② - ①得:$5h-3h=2x + 20-(2x + 6)$,$2h = 14$,解得$h = 7$。
路灯杆$AB$的高度为$7\ \mathrm{m}$。
17. (10 分)一根旗杆的高为 $ 6m $,影长为 $ 8m $,在同一时刻,一幢建筑物的影长为 $ 16m $,求建筑物的顶端与它的影子的顶端之间的距离.
答案:17. 20 m.
解析:
设建筑物的高为$h$。
同一时刻,物体高度与影长成正比,可得$\frac{6}{8}=\frac{h}{16}$,解得$h = 12\space m$。
建筑物的顶端与影子顶端的距离为直角三角形的斜边,两直角边分别为建筑物高度$12\space m$和影长$16\space m$,根据勾股定理,距离为$\sqrt{12^{2}+16^{2}}=\sqrt{144 + 256}=\sqrt{400}=20\space m$。
20 m
同一时刻,物体高度与影长成正比,可得$\frac{6}{8}=\frac{h}{16}$,解得$h = 12\space m$。
建筑物的顶端与影子顶端的距离为直角三角形的斜边,两直角边分别为建筑物高度$12\space m$和影长$16\space m$,根据勾股定理,距离为$\sqrt{12^{2}+16^{2}}=\sqrt{144 + 256}=\sqrt{400}=20\space m$。
20 m
18. (8 分)某种药品包装盒的侧面展开图如图所示,如果长方体盒子的长比宽多 $ 4cm $,求这种药品包装盒的体积.


答案:18. 90 cm³.
解析:
设这种药品包装盒的宽为$x\ \mathrm{cm}$,则长为$(x + 4)\ \mathrm{cm}$,高为$y\ \mathrm{cm}$。
根据侧面展开图,可得方程组:
$\begin{cases}2y + x + (x + 4) = 14 \\x + 4 + 2y = 13\end{cases}$
由第二个方程得:$x + 2y = 9$,代入第一个方程:$9 + x = 14$,解得$x = 5$。
则长为$5 + 4 = 9\ \mathrm{cm}$,代入$x + 2y = 9$,得$5 + 2y = 9$,解得$y = 2$。
体积为$9×5×2 = 90\ \mathrm{cm}^3$。
90$\mathrm{cm}^3$
根据侧面展开图,可得方程组:
$\begin{cases}2y + x + (x + 4) = 14 \\x + 4 + 2y = 13\end{cases}$
由第二个方程得:$x + 2y = 9$,代入第一个方程:$9 + x = 14$,解得$x = 5$。
则长为$5 + 4 = 9\ \mathrm{cm}$,代入$x + 2y = 9$,得$5 + 2y = 9$,解得$y = 2$。
体积为$9×5×2 = 90\ \mathrm{cm}^3$。
90$\mathrm{cm}^3$
19. 某一个周末张明去爸爸的工作室玩,张明发现爸爸桌面上设计的某个零件的三视图如下图所示,爸爸见张明对设计图纸如此感兴趣就考了张明如下几个问题,你能帮张明解决这些问题吗?

(1)此物体是
(2)请你求出此物体的表面积;
(3)如果这个零件是用来支撑圆桌的,在圆桌的正上方有一盏吊灯,在灯光下,圆桌在地板上的投影是面积为 $ 0.81π m^2 $ 的圆. 已知圆桌的高度为 $ 1m $,圆桌面的半径为 $ 0.5m $,求吊灯距地面的高度.

(1)此物体是
圆柱
;(2)请你求出此物体的表面积;
(3)如果这个零件是用来支撑圆桌的,在圆桌的正上方有一盏吊灯,在灯光下,圆桌在地板上的投影是面积为 $ 0.81π m^2 $ 的圆. 已知圆桌的高度为 $ 1m $,圆桌面的半径为 $ 0.5m $,求吊灯距地面的高度.
答案:19. (1) 圆柱;(2) 1000π;(3) $\frac{9}{4}$m.
解析:
(1) 圆柱
(2) 解:由三视图可知,圆柱底面直径为20,高为40,
则底面半径 $ r = 10 $,
表面积 $ S = 2π r^2 + 2π rh = 2π × 10^2 + 2π × 10 × 40 = 200π + 800π = 1000π $
(3) 解:设吊灯距地面高度为 $ h \, \mathrm{m} $,
圆桌投影圆面积为 $ 0.81π \, \mathrm{m}^2 $,则投影圆半径 $ R = \sqrt{\frac{0.81π}{π}} = 0.9 \, \mathrm{m} $,
由相似三角形得 $ \frac{0.5}{0.9} = \frac{h - 1}{h} $,
解得 $ h = \frac{9}{4} $
(2) 解:由三视图可知,圆柱底面直径为20,高为40,
则底面半径 $ r = 10 $,
表面积 $ S = 2π r^2 + 2π rh = 2π × 10^2 + 2π × 10 × 40 = 200π + 800π = 1000π $
(3) 解:设吊灯距地面高度为 $ h \, \mathrm{m} $,
圆桌投影圆面积为 $ 0.81π \, \mathrm{m}^2 $,则投影圆半径 $ R = \sqrt{\frac{0.81π}{π}} = 0.9 \, \mathrm{m} $,
由相似三角形得 $ \frac{0.5}{0.9} = \frac{h - 1}{h} $,
解得 $ h = \frac{9}{4} $