8. 若$\sin45^{\circ}=\cos\beta$,则锐角β的度数为
45
°。答案:45
9. 如图,网格图中每个小正方形的面积都为1。经过格点A的直线MN把网格图分成了两部分,其中△BMN的面积为3,则$\sin\angle MNB$的值为

$\frac{\sqrt{6}-\sqrt{2}}{4}$
。
答案:9.$\frac{\sqrt{6}-\sqrt{2}}{4}$
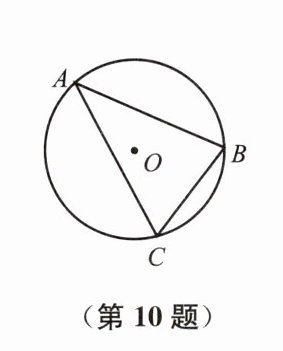
10. 如图,△ABC内接于⊙O,若$\sin\angle BAC=\frac{1}{3}$,$BC=2\sqrt{6}$,则⊙O的半径为
$3\sqrt{6}$
。
答案:$3\sqrt{6}$
11. 在△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,若$b^{2}=2ac$,则$\sin A$的值为
$\sqrt{2}-1$
。答案:$\sqrt{2}-1$
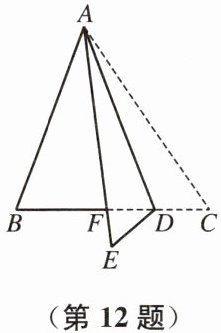
12. 如图,在△ABC中,$\tan C=\frac{4}{3}$,D是边BC上一点,将△ACD沿AD翻折得到△AED,线段AE、BC相交于点F。若CF=5,EF=2,则AC=
$\frac{21}{2}$
。
答案:12.$\frac{21}{2}$
解析:
证明:设 $ AC = AE = x $,则 $ AF = AE - EF = x - 2 $。
过点 $ A $ 作 $ AH ⊥ BC $ 于点 $ H $,设 $ AH = 4k $,$ CH = 3k $,由勾股定理得 $ AC = 5k $,即 $ x = 5k $,$ CH = 3k $。
在 $ \mathrm{Rt}\triangle AFH $ 中,$ FH = CH - CF = 3k - 5 $,$ AF = x - 2 = 5k - 2 $,$ AH = 4k $,由勾股定理得:
$(3k - 5)^2 + (4k)^2 = (5k - 2)^2$
展开并化简:
$9k^2 - 30k + 25 + 16k^2 = 25k^2 - 20k + 4$
$25k^2 - 30k + 25 = 25k^2 - 20k + 4$
$-10k = -21 \implies k = \frac{21}{10}$
则 $ AC = 5k = 5 × \frac{21}{10} = \frac{21}{2} $。
$\frac{21}{2}$
过点 $ A $ 作 $ AH ⊥ BC $ 于点 $ H $,设 $ AH = 4k $,$ CH = 3k $,由勾股定理得 $ AC = 5k $,即 $ x = 5k $,$ CH = 3k $。
在 $ \mathrm{Rt}\triangle AFH $ 中,$ FH = CH - CF = 3k - 5 $,$ AF = x - 2 = 5k - 2 $,$ AH = 4k $,由勾股定理得:
$(3k - 5)^2 + (4k)^2 = (5k - 2)^2$
展开并化简:
$9k^2 - 30k + 25 + 16k^2 = 25k^2 - 20k + 4$
$25k^2 - 30k + 25 = 25k^2 - 20k + 4$
$-10k = -21 \implies k = \frac{21}{10}$
则 $ AC = 5k = 5 × \frac{21}{10} = \frac{21}{2} $。
$\frac{21}{2}$
三、解答题(共52分)
13. (10分)如图,∠MON=60°,以O为圆心,2为半径画弧,分别交OM、ON于A、B两点,再分别以A、B为圆心,$\sqrt{6}$为半径画弧,两弧在∠MON内部相交于点C,作射线OC,连接AC、BC,求$\tan\angle BCO$的值。
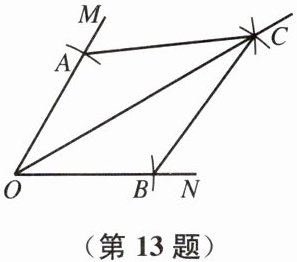
13. (10分)如图,∠MON=60°,以O为圆心,2为半径画弧,分别交OM、ON于A、B两点,再分别以A、B为圆心,$\sqrt{6}$为半径画弧,两弧在∠MON内部相交于点C,作射线OC,连接AC、BC,求$\tan\angle BCO$的值。

答案:13.$\frac{\sqrt{5}}{5}$
解析:
解:连接OA、OB,过点C作CD⊥ON于点D。
∵OA=OB=2,∠MON=60°,
∴△OAB为等边三角形,
∴∠OBA=60°,AB=OA=2。
∵AC=BC=$\sqrt{6}$,
∴OC垂直平分AB,设OC与AB交于点E,
则AE=EB=1,OE⊥AB。
在Rt△OEB中,OE=OB·cos60°=2×$\frac{1}{2}$=1,
EB=1,
在Rt△CEB中,CE=$\sqrt{BC^2 - EB^2}=\sqrt{(\sqrt{6})^2 - 1^2}=\sqrt{5}$,
∴OC=OE + CE=1 + $\sqrt{5}$。
设OD=x,CD=y,在Rt△OCD中,OC²=OD² + CD²,即$(1 + \sqrt{5})^2 = x^2 + y^2$,
在Rt△BCD中,BC²=BD² + CD²,OB=2,BD=OD - OB=x - 2,
则$(\sqrt{6})^2=(x - 2)^2 + y^2$。
联立方程:$\begin{cases}(1 + \sqrt{5})^2 = x^2 + y^2 \\ 6=(x - 2)^2 + y^2\end{cases}$,
两式相减得:$(1 + 2\sqrt{5} + 5) - 6 = x^2 - (x^2 - 4x + 4)$,
化简得:$2\sqrt{5} = 4x - 4$,解得$x = 1 + \frac{\sqrt{5}}{2}$。
代入$6=(x - 2)^2 + y^2$,得$6=(\frac{\sqrt{5}}{2} - 1)^2 + y^2$,
解得$y = \frac{\sqrt{5}(\sqrt{5} + 2)}{2}$(负值舍去)。
在Rt△CDO中,OD=$1 + \frac{\sqrt{5}}{2}$,OC=$1 + \sqrt{5}$,
则CD=$\frac{\sqrt{5}(\sqrt{5} + 2)}{2}$,OD=$1 + \frac{\sqrt{5}}{2}$,
∴BD=OD - OB=$\frac{\sqrt{5}}{2} - 1$。
在Rt△BCD中,$\tan\angle BCO = \frac{BD}{CD} = \frac{\frac{\sqrt{5}}{2} - 1}{\frac{\sqrt{5}(\sqrt{5} + 2)}{2}} = \frac{\sqrt{5} - 2}{5 + 2\sqrt{5}} = \frac{(\sqrt{5} - 2)(5 - 2\sqrt{5})}{(5 + 2\sqrt{5})(5 - 2\sqrt{5})} = \frac{\sqrt{5}}{5}$。
$\tan\angle BCO$的值为$\frac{\sqrt{5}}{5}$。
∵OA=OB=2,∠MON=60°,
∴△OAB为等边三角形,
∴∠OBA=60°,AB=OA=2。
∵AC=BC=$\sqrt{6}$,
∴OC垂直平分AB,设OC与AB交于点E,
则AE=EB=1,OE⊥AB。
在Rt△OEB中,OE=OB·cos60°=2×$\frac{1}{2}$=1,
EB=1,
在Rt△CEB中,CE=$\sqrt{BC^2 - EB^2}=\sqrt{(\sqrt{6})^2 - 1^2}=\sqrt{5}$,
∴OC=OE + CE=1 + $\sqrt{5}$。
设OD=x,CD=y,在Rt△OCD中,OC²=OD² + CD²,即$(1 + \sqrt{5})^2 = x^2 + y^2$,
在Rt△BCD中,BC²=BD² + CD²,OB=2,BD=OD - OB=x - 2,
则$(\sqrt{6})^2=(x - 2)^2 + y^2$。
联立方程:$\begin{cases}(1 + \sqrt{5})^2 = x^2 + y^2 \\ 6=(x - 2)^2 + y^2\end{cases}$,
两式相减得:$(1 + 2\sqrt{5} + 5) - 6 = x^2 - (x^2 - 4x + 4)$,
化简得:$2\sqrt{5} = 4x - 4$,解得$x = 1 + \frac{\sqrt{5}}{2}$。
代入$6=(x - 2)^2 + y^2$,得$6=(\frac{\sqrt{5}}{2} - 1)^2 + y^2$,
解得$y = \frac{\sqrt{5}(\sqrt{5} + 2)}{2}$(负值舍去)。
在Rt△CDO中,OD=$1 + \frac{\sqrt{5}}{2}$,OC=$1 + \sqrt{5}$,
则CD=$\frac{\sqrt{5}(\sqrt{5} + 2)}{2}$,OD=$1 + \frac{\sqrt{5}}{2}$,
∴BD=OD - OB=$\frac{\sqrt{5}}{2} - 1$。
在Rt△BCD中,$\tan\angle BCO = \frac{BD}{CD} = \frac{\frac{\sqrt{5}}{2} - 1}{\frac{\sqrt{5}(\sqrt{5} + 2)}{2}} = \frac{\sqrt{5} - 2}{5 + 2\sqrt{5}} = \frac{(\sqrt{5} - 2)(5 - 2\sqrt{5})}{(5 + 2\sqrt{5})(5 - 2\sqrt{5})} = \frac{\sqrt{5}}{5}$。
$\tan\angle BCO$的值为$\frac{\sqrt{5}}{5}$。