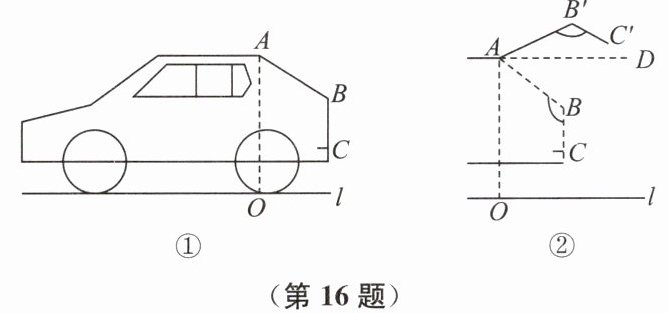
16. (10分)图①是某越野车的侧面示意图,折线段ABC表示车后盖,已知AB=1m,BC=0.6m,∠ABC=123°,该车的高度AO=1.7m。如图②,打开后备箱,车后盖ABC落在AB'C'处,AB'与水平面的夹角∠B'AD=27°。
(1)求打开后备箱后,车后盖最高点B'到地面l的距离。
(2)若小琳爸爸的身高为1.8m,他从打开的车后盖C'处经过,有没有碰头的危险?请说明理由。(精确到0.01m;参考数据:$\sin27^{\circ}\approx0.454$,$\cos27^{\circ}\approx0.891$,$\tan27^{\circ}\approx0.510$,$\sqrt{3}\approx1.732$)
(1)求打开后备箱后,车后盖最高点B'到地面l的距离。
(2)若小琳爸爸的身高为1.8m,他从打开的车后盖C'处经过,有没有碰头的危险?请说明理由。(精确到0.01m;参考数据:$\sin27^{\circ}\approx0.454$,$\cos27^{\circ}\approx0.891$,$\tan27^{\circ}\approx0.510$,$\sqrt{3}\approx1.732$)

答案:
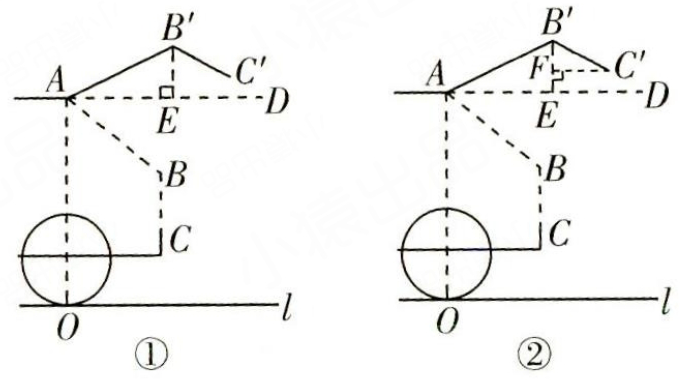
解:(1)如图①,作B'E⊥AD,垂足为E.
在Rt△AB'E中,
因为∠B'AD=27°,
$AB'=AB=1\ \mathrm {m}$
所以$sin 27°=\frac {B'E}{AB'}$
所以$B'E=AB'sin 27°≈1×0.454=0. 454(\mathrm {m}).$
因为平行线间的距离处处相等,
所以$B'E+AO=0.454+1.7=2.154≈2.15(\mathrm {m}).$
答:车后盖最高点B'到地面l的距离约为$2.15\ \mathrm {m}.$
(2)没有碰头的危险,理由如下:
如图②,过点C作C'F⊥B'E.垂足为F.
因为∠B'AD=27°,∠B'EA =90°,
所以∠AB'E = 63°.
因为∠AB'C'=∠ABC= 123°,
所以∠C'B'F=∠AB'C'-∠AB'E = 60°.
在Rt△B'FC'中,$B'C'= BC=0.6\ \mathrm {m}. .$
所以$B'F=B'C'×cos 60° = 0.3(\mathrm {m}).$
因为平行线间的距离处处相等,.
所以点C到地面的距离为$2. 15-0.3= 1.85(\mathrm {m}).$
因为$1.85\gt 1.8.$
所以没有碰头的危险.
解:(1)如图①,作B'E⊥AD,垂足为E.
在Rt△AB'E中,
因为∠B'AD=27°,
$AB'=AB=1\ \mathrm {m}$
所以$sin 27°=\frac {B'E}{AB'}$
所以$B'E=AB'sin 27°≈1×0.454=0. 454(\mathrm {m}).$
因为平行线间的距离处处相等,
所以$B'E+AO=0.454+1.7=2.154≈2.15(\mathrm {m}).$
答:车后盖最高点B'到地面l的距离约为$2.15\ \mathrm {m}.$
(2)没有碰头的危险,理由如下:
如图②,过点C作C'F⊥B'E.垂足为F.
因为∠B'AD=27°,∠B'EA =90°,
所以∠AB'E = 63°.
因为∠AB'C'=∠ABC= 123°,
所以∠C'B'F=∠AB'C'-∠AB'E = 60°.
在Rt△B'FC'中,$B'C'= BC=0.6\ \mathrm {m}. .$
所以$B'F=B'C'×cos 60° = 0.3(\mathrm {m}).$
因为平行线间的距离处处相等,.
所以点C到地面的距离为$2. 15-0.3= 1.85(\mathrm {m}).$
因为$1.85\gt 1.8.$
所以没有碰头的危险.

17. (12分)【阅读材料】在锐角△ABC中,∠A、∠B、∠C的对边长分别为a、b、c,则$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$。这是关于三角形的重要结论,可用于解决实际问题。
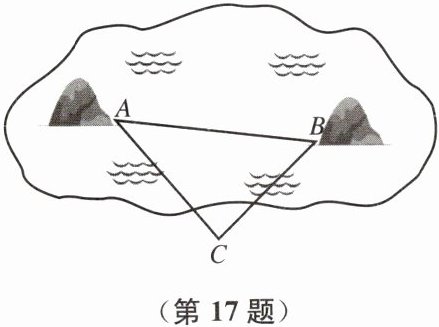
【问题提出】某工程小组要绘制一湖泊的平面示意图,需要知道湖中A、B两岛之间的实际距离。由于地形原因,无法利用测距仪直接测量,该小组对这一问题进行了探究。
【方案设计】工具:测距仪、无人机(只能测量角度、水平面高度)。
测量过程:①如图,在空旷地面找一点C;
②利用无人机多次测量并取平均值,得∠A≈43°,∠B≈51°;
③利用测距仪多次测量并取平均值,得BC≈341m,AC≈388.5m。
【问题解决】(1)请计算A、B两岛之间的距离。(参考数据:$\sin43^{\circ}\approx0.682$,$\sin51^{\circ}\approx0.777$,$\sin86^{\circ}\approx0.998$)
【评价反思】(2)请设计其他方案计算A、B两岛间的距离。
【问题提出】某工程小组要绘制一湖泊的平面示意图,需要知道湖中A、B两岛之间的实际距离。由于地形原因,无法利用测距仪直接测量,该小组对这一问题进行了探究。
【方案设计】工具:测距仪、无人机(只能测量角度、水平面高度)。
测量过程:①如图,在空旷地面找一点C;
②利用无人机多次测量并取平均值,得∠A≈43°,∠B≈51°;
③利用测距仪多次测量并取平均值,得BC≈341m,AC≈388.5m。
【问题解决】(1)请计算A、B两岛之间的距离。(参考数据:$\sin43^{\circ}\approx0.682$,$\sin51^{\circ}\approx0.777$,$\sin86^{\circ}\approx0.998$)
【评价反思】(2)请设计其他方案计算A、B两岛间的距离。

答案:17.(1)499m;(2)略
解析:
(1)在△ABC中,∠A≈43°,∠B≈51°,则∠C=180°-∠A-∠B≈180°-43°-51°=86°。
由正弦定理可得:$\frac{AB}{\sin C}=\frac{BC}{\sin A}$。
已知BC≈341m,$\sin A≈0.682$,$\sin C≈0.998$,则$AB=\frac{BC · \sin C}{\sin A}≈\frac{341×0.998}{0.682}≈\frac{340.318}{0.682}≈499$m。
(2)在湖边选一点C,测量∠ACB的度数,再测量AC和BC的长度,利用余弦定理$AB^2=AC^2 + BC^2 - 2AC · BC · \cos∠ACB$计算AB的距离。
由正弦定理可得:$\frac{AB}{\sin C}=\frac{BC}{\sin A}$。
已知BC≈341m,$\sin A≈0.682$,$\sin C≈0.998$,则$AB=\frac{BC · \sin C}{\sin A}≈\frac{341×0.998}{0.682}≈\frac{340.318}{0.682}≈499$m。
(2)在湖边选一点C,测量∠ACB的度数,再测量AC和BC的长度,利用余弦定理$AB^2=AC^2 + BC^2 - 2AC · BC · \cos∠ACB$计算AB的距离。