8. 一只不透明的袋子中装有 4 个小球,分别标有 2、3、4、$x$,这些球除数字外都相同. 甲每次从袋中随机摸出两个小球,并计算摸出的这两个小球上的数字之和. 记录后将小球放回袋中搅匀,进行重复试验. 试验数据如下表:

(1) 如果试验继续进行下去,根据上表数据,出现“和为 7”的频率将稳定在它的概率附近,试估计出现“和为 7”的概率;
(2) 根据第(1)题,若 $x$ 是不等于 2、3、4 的自然数,试求 $x$ 的值.

(1) 如果试验继续进行下去,根据上表数据,出现“和为 7”的频率将稳定在它的概率附近,试估计出现“和为 7”的概率;
(2) 根据第(1)题,若 $x$ 是不等于 2、3、4 的自然数,试求 $x$ 的值.
答案:
解:(1) 出现和为7的概率是0.33
(2)列表如下
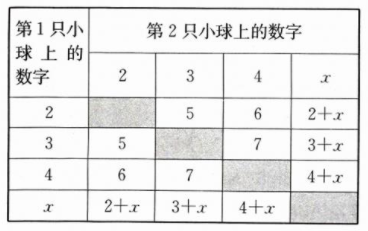
一共有12种可能的结果
由(1)知,出现和为7的概率约为0.33
∴和为7出现的次数为0.33×12=3.96≈4
若2+x=7,则x=5,此时P(和为$7)=\frac {1}{3} ≈0.33,$符合题意
若3+x=7,则x=4,不符合题意
若4+x=7,则x=3,不符合题意
∴x=5
解:(1) 出现和为7的概率是0.33
(2)列表如下

一共有12种可能的结果
由(1)知,出现和为7的概率约为0.33
∴和为7出现的次数为0.33×12=3.96≈4
若2+x=7,则x=5,此时P(和为$7)=\frac {1}{3} ≈0.33,$符合题意
若3+x=7,则x=4,不符合题意
若4+x=7,则x=3,不符合题意
∴x=5
9. 在 4 件同型号的产品中,其中,1 件不合格品,3 件合格品.
(1) 从这 4 件产品中随机抽取 1 件进行检测,求抽到的是不合格品的概率.
(2) 从这 4 件产品中随机抽取 2 件进行检测,求抽到的都是合格品的概率.
(3) 在这 4 件产品中加入 $x$ 件合格品后,进行如下试验:随机抽取 1 件进行检测,然后放回,多次重复这个试验. 通过大量重复试验后发现,抽到合格品的频率稳定在 0.95,试估计 $x$ 的值.
(1) 从这 4 件产品中随机抽取 1 件进行检测,求抽到的是不合格品的概率.
(2) 从这 4 件产品中随机抽取 2 件进行检测,求抽到的都是合格品的概率.
(3) 在这 4 件产品中加入 $x$ 件合格品后,进行如下试验:随机抽取 1 件进行检测,然后放回,多次重复这个试验. 通过大量重复试验后发现,抽到合格品的频率稳定在 0.95,试估计 $x$ 的值.
答案:
解:(1)P(抽到的是不合格品$)=\frac {1}{1+3}=\frac {1}{4}$
(2)树状图如下
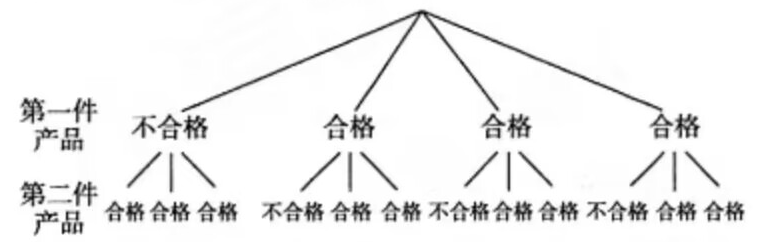
共有12种等可能的情况,其中抽到的都是合格品的情况有6种
∴P(抽到的都是合格品$)=\frac{6}{12}=\frac{1}{2}$
(3) 由题意,得$ \frac{3+x}{4+x}=0.95 $
解得x=16
∴x的值大约是16
解:(1)P(抽到的是不合格品$)=\frac {1}{1+3}=\frac {1}{4}$
(2)树状图如下

共有12种等可能的情况,其中抽到的都是合格品的情况有6种
∴P(抽到的都是合格品$)=\frac{6}{12}=\frac{1}{2}$
(3) 由题意,得$ \frac{3+x}{4+x}=0.95 $
解得x=16
∴x的值大约是16