6. 把标有号码 $ 1,2,3,···,10 $ 的 $ 10 $ 个乒乓球放在一只不透明的箱子中,摇匀后从中任意取一个,所得乒乓球的号码为小于 $ 7 $ 的奇数的概率是(
A.$\frac{3}{10}$
B.$\frac{7}{10}$
C.$\frac{2}{5}$
D.$\frac{3}{5}$
A
).A.$\frac{3}{10}$
B.$\frac{7}{10}$
C.$\frac{2}{5}$
D.$\frac{3}{5}$
答案:A
7. 一只不透明的盒中装有若干个除颜色外都相同的红球与黄球. 先从盒中摸出 $ 8 $ 个球,画上记号放回盒中,再进行摸球试验. 摸球试验的要求:先搅拌均匀,每次摸出 $ 1 $ 个球,记录后放回盒中,再继续. 摸球试验一共做了 $ 50 $ 次,结果如下:

(1) 估计盒中红球、黄球约占小球总数的百分比分别是多少.
(2) 估计盒中有红球多少个.

(1) 估计盒中红球、黄球约占小球总数的百分比分别是多少.
(2) 估计盒中有红球多少个.
答案:解:(1)50次摸球试验中,出现红球20次,黄球30次
由此估计,红球约占40\%,黄球约占60\%
$ (2)8÷\frac {2+2}{50}×40%=40($个)
∴红球约有40个
由此估计,红球约占40\%,黄球约占60\%
$ (2)8÷\frac {2+2}{50}×40%=40($个)
∴红球约有40个
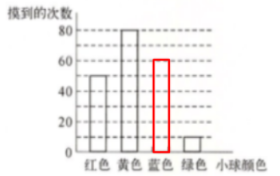
8. 一只不透明的口袋中装有若干个红、黄、蓝、绿 $ 4 $ 种颜色的小球,小球除颜色外完全相同,为估计该口袋中 $ 4 $ 种颜色的小球数量,每次从口袋中随机摸出一球记下颜色并放回,重复多次试验,汇总摸球结果绘制成如下不完整的条形统计图和扇形统计图.

根据以上信息,解答下列问题:
(1) 求试验总次数,并补全条形统计图.
(2) 在扇形统计图中,“黄球”对应的扇形圆心角为多少度?
(3) 已知该口袋中有 $ 10 $ 个红球,估计口袋中绿球的数量.

根据以上信息,解答下列问题:
(1) 求试验总次数,并补全条形统计图.
(2) 在扇形统计图中,“黄球”对应的扇形圆心角为多少度?
(3) 已知该口袋中有 $ 10 $ 个红球,估计口袋中绿球的数量.
答案:
解: (1)试验总次数: 50÷25\%=200(次)
摸到蓝球的次数: 200-50-80-10=60(次)
答:试验总次数为200次。
(2)“黄球” 所占百分比: 80÷200=40\%
对应的扇形圆心角度数: 40\%× 360° = 144°
答:“黄球”对应的扇形圆心角度数为144°
$(3)10×\frac {10}{50}= 2($个)
答:估计口袋中绿球的数量为2个。
解: (1)试验总次数: 50÷25\%=200(次)
摸到蓝球的次数: 200-50-80-10=60(次)
答:试验总次数为200次。
(2)“黄球” 所占百分比: 80÷200=40\%
对应的扇形圆心角度数: 40\%× 360° = 144°
答:“黄球”对应的扇形圆心角度数为144°
$(3)10×\frac {10}{50}= 2($个)
答:估计口袋中绿球的数量为2个。
