9. 摄影时,为了寻找拍摄画面中的黄金分割点,摄影师常大致构造一个黄金矩形:在正方形$ABCD$中,以$AB$的中点$E$为圆心,线段$EC$为半径画弧,交$AB$的延长线于点$F$,图中便出现了黄金矩形. 请指出图中的黄金分割点和黄金矩形,并加以说明.


答案:解:B为线段AF的黄金分割点,C为线段DG的黄金分割点,
矩形AFGD和矩形CBFG都是黄金矩形,证明如下:
设正方形ABCD的边长为a,则AB=BC=a
∵点E是AB的中点
∴$BE=\frac 12AB=\frac {a}2$
在Rt△BCE中,∵$BE=\frac {a}2,$BC=a
∴$CE=\sqrt {BE^2+BC^2}=\frac {\sqrt 5}2a$
∴$EF=\frac {\sqrt 5}2a,$$AF=\frac {\sqrt 5+1}2a,$$BF=\frac {\sqrt 5-1}2a$
∴$\frac {AB}{AF}=\frac a{\frac {\sqrt 5+1}2a}=\frac {\sqrt 5-1}2≈0.618$
∴点B是线段AF的黄金分割点
∵$\frac {DC}{DG}=\frac {AB}{AF}≈0.618$
∴点C是线段DG的黄金分割点
∵$\frac {AD}{AF}=\frac {AB}{AF}≈0.618,$$\frac {BF}{BC}=\frac {\frac {\sqrt 5-1}2a}{a}=\frac {\sqrt 5-1}2≈0.618$
∴矩形AFGD和矩形CBFG都是黄金矩形
矩形AFGD和矩形CBFG都是黄金矩形,证明如下:
设正方形ABCD的边长为a,则AB=BC=a
∵点E是AB的中点
∴$BE=\frac 12AB=\frac {a}2$
在Rt△BCE中,∵$BE=\frac {a}2,$BC=a
∴$CE=\sqrt {BE^2+BC^2}=\frac {\sqrt 5}2a$
∴$EF=\frac {\sqrt 5}2a,$$AF=\frac {\sqrt 5+1}2a,$$BF=\frac {\sqrt 5-1}2a$
∴$\frac {AB}{AF}=\frac a{\frac {\sqrt 5+1}2a}=\frac {\sqrt 5-1}2≈0.618$
∴点B是线段AF的黄金分割点
∵$\frac {DC}{DG}=\frac {AB}{AF}≈0.618$
∴点C是线段DG的黄金分割点
∵$\frac {AD}{AF}=\frac {AB}{AF}≈0.618,$$\frac {BF}{BC}=\frac {\frac {\sqrt 5-1}2a}{a}=\frac {\sqrt 5-1}2≈0.618$
∴矩形AFGD和矩形CBFG都是黄金矩形
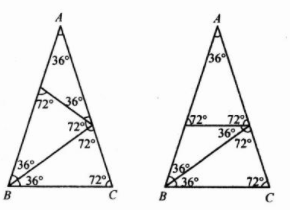
10. 在$\triangle ABC$中,$AB = AC$,$\angle A = 36^{\circ}$,像这样,顶角为$36^{\circ}$的等腰三角形称为黄金三角形.
(1)请你利用图①和图②设计两种不同的分法,将黄金三角形$ABC$分割成三个等腰三角形,使分成的三角形中含有两个黄金三角形(标出所得三角形的内角度数,不要求写画法);
(2)在图③中,$BF$平分$\angle ABC$交$AC$于点$F$,取$AB$的中点$E$,连接$EF$并延长交$BC$的延长线于点$M$. 判断$CM$与$AB$之间的数量关系,并说明理由.

(1)请你利用图①和图②设计两种不同的分法,将黄金三角形$ABC$分割成三个等腰三角形,使分成的三角形中含有两个黄金三角形(标出所得三角形的内角度数,不要求写画法);
(2)在图③中,$BF$平分$\angle ABC$交$AC$于点$F$,取$AB$的中点$E$,连接$EF$并延长交$BC$的延长线于点$M$. 判断$CM$与$AB$之间的数量关系,并说明理由.

答案:
解:(1)如图所示
$(2)\ \mathrm {CM}=AB,$理由如下:
连接MA
∵∠BAC=36°,AB=AC
∴∠ABC=∠ACB=72°
∵BF 平分∠ABC
∴∠l=∠2=36°
∵∠1=∠BAC
∴BF=AF,△ABF 为等腰三角形
∵E是AB中点
∴FE⊥AB
∴ME是AB的垂直平分线
∴MA =MB
∴∠MAB=∠MBA=72°
∵∠BAC=36°
∴∠MAC=36°
∵∠ACB=72°
∴∠AMC=36°=∠MAC
∴CM=AC=AB
解:(1)如图所示
$(2)\ \mathrm {CM}=AB,$理由如下:
连接MA
∵∠BAC=36°,AB=AC
∴∠ABC=∠ACB=72°
∵BF 平分∠ABC
∴∠l=∠2=36°
∵∠1=∠BAC
∴BF=AF,△ABF 为等腰三角形
∵E是AB中点
∴FE⊥AB
∴ME是AB的垂直平分线
∴MA =MB
∴∠MAB=∠MBA=72°
∵∠BAC=36°
∴∠MAC=36°
∵∠ACB=72°
∴∠AMC=36°=∠MAC
∴CM=AC=AB

11. 用纸折出黄金分割点:在一张正方形纸片$ABCD$中,先折出边$BC$的中点$E$,再折出线段$AE$,然后通过折叠使线段$EB$落在线段$EA$上,点$B$落在点$B'$处,$EB' = EB$;类似地,在$AB$上找出点$B''$,使$AB'' = AB'$(如图). 这时点$B''$就是$AB$的黄金分割点. 请说明理由.


答案:解:设BE=1,则BC=AB=2,$AE=\sqrt{AB^2+BE^2}=\sqrt 5$
∵EB'=EB
∴$AB''=AB'=\sqrt{5} -1$
∴$AB''∶AB=(\sqrt{5} -1)∶2$
∴B''是AB的黄金分割点
∵EB'=EB
∴$AB''=AB'=\sqrt{5} -1$
∴$AB''∶AB=(\sqrt{5} -1)∶2$
∴B''是AB的黄金分割点