8. 小明和同学做影子游戏时发现,对于同一物体,影子的大小与光源到物体的距离有关. 因此,他们认为可以借助物体影子的长度计算光源到物体的位置.
(1) 如图①,垂直于地面放置的正方形框架 $ ABCD $,$ AB $ 为 $ 30$ cm,在其正上方点 $ P $ 处有一灯泡,在灯泡的照射下,正方形框架的横向影子 $ A'B、D'C $ 长度的和为 $ 6$ cm. 灯泡离地面的高度为多少?
(2) 不改变图①中灯泡的位置,将两个边长为 $ 30$ cm 的正方形框架按图②摆放,请计算此时横向影子 $ A'B、D'C $ 长度的和为多少.
(3) 有 $ n $ 个边长为 $ a $ 的正方形按图③摆放,测得横向影子 $ A'B、D'C $ 长度的和为 $ b $,求灯泡离地面的距离. (写出解题过程,结果用含 $ a、b、n $ 的代数式表示)

(1) 如图①,垂直于地面放置的正方形框架 $ ABCD $,$ AB $ 为 $ 30$ cm,在其正上方点 $ P $ 处有一灯泡,在灯泡的照射下,正方形框架的横向影子 $ A'B、D'C $ 长度的和为 $ 6$ cm. 灯泡离地面的高度为多少?
(2) 不改变图①中灯泡的位置,将两个边长为 $ 30$ cm 的正方形框架按图②摆放,请计算此时横向影子 $ A'B、D'C $ 长度的和为多少.
(3) 有 $ n $ 个边长为 $ a $ 的正方形按图③摆放,测得横向影子 $ A'B、D'C $ 长度的和为 $ b $,求灯泡离地面的距离. (写出解题过程,结果用含 $ a、b、n $ 的代数式表示)

答案:
解:(1)如图,
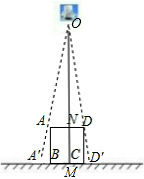
∵AB∥OM,
∴△A′AB∽△A′OM,
∴$\frac{A′B}{A′M}=\frac{AB}{OM},$
即$\frac{A′B}{A′B+BM}=\frac{30}{OM}①,$
∵DC∥OM,
∴△D′DC∽△D′OM,
∴$\frac{D′C}{D′M}=\frac{CD}{OM},$
即$\frac{D′C}{D′C+CM}=\frac{30}{OM}②,$
由①②得$\frac{A′B}{A′B+BM}=\frac{D′C}{D′C+CM},$
∴$\frac{A′B}{A′B+BM}=\frac{D′C}{D′C+CM}=\frac{A′B+D′C}{A′B+BM+CM+D′C}=\frac{6}{30+6}=\frac{1}{6},$
∴$\frac{30}{OM}=\frac{1}{6},$
∴$OM=180(\ \mathrm {cm})$
解:(2)设横向影子A'B,D'C的长度和为$y\ \mathrm {cm},$
同理可得$\frac {60}{60+y}=\frac {150}{180},$
解得$y=12\ \mathrm {cm}.$
解:(3)记灯泡为点P,如图:
∵AD//A'D',
∴∠PAD=∠PA'D',∠PDA=∠PD'A'.
∴△PAD∽△PA'D'.
根据相似三角形对应高的比等于相似比,
可得$\frac {AD}{A'D'}=\frac {PN}{PM},$
设灯泡离地面距离为x,
由题意得PM=x,PN=x-a,AD=na,A'D'=na+b,
∴$\frac {na}{na+b}=\frac {x-a}x=1-\frac ax$
$\frac ax=1-\frac {na}{na+b}$
$x=\frac {na^2+ab}b.$
解:(1)如图,

∵AB∥OM,
∴△A′AB∽△A′OM,
∴$\frac{A′B}{A′M}=\frac{AB}{OM},$
即$\frac{A′B}{A′B+BM}=\frac{30}{OM}①,$
∵DC∥OM,
∴△D′DC∽△D′OM,
∴$\frac{D′C}{D′M}=\frac{CD}{OM},$
即$\frac{D′C}{D′C+CM}=\frac{30}{OM}②,$
由①②得$\frac{A′B}{A′B+BM}=\frac{D′C}{D′C+CM},$
∴$\frac{A′B}{A′B+BM}=\frac{D′C}{D′C+CM}=\frac{A′B+D′C}{A′B+BM+CM+D′C}=\frac{6}{30+6}=\frac{1}{6},$
∴$\frac{30}{OM}=\frac{1}{6},$
∴$OM=180(\ \mathrm {cm})$
解:(2)设横向影子A'B,D'C的长度和为$y\ \mathrm {cm},$
同理可得$\frac {60}{60+y}=\frac {150}{180},$
解得$y=12\ \mathrm {cm}.$
解:(3)记灯泡为点P,如图:
∵AD//A'D',
∴∠PAD=∠PA'D',∠PDA=∠PD'A'.
∴△PAD∽△PA'D'.
根据相似三角形对应高的比等于相似比,
可得$\frac {AD}{A'D'}=\frac {PN}{PM},$
设灯泡离地面距离为x,
由题意得PM=x,PN=x-a,AD=na,A'D'=na+b,
∴$\frac {na}{na+b}=\frac {x-a}x=1-\frac ax$
$\frac ax=1-\frac {na}{na+b}$
$x=\frac {na^2+ab}b.$
9. 如图①,小明晚上在路灯下散步. 已知小明的身高 $ AB = h $,灯柱的高 $ OP = O'P' = l $,两灯柱之间的距离 $ OO' = m $.
(1) 若小明距灯柱 $ OP $ 的水平距离 $ OA = a $,则他的影长 $ AC = $
(2) 若小明在两路灯之间行走,则他前后的两个影子的长度之和($ AC + AD $)是否不断改变? 为什么?
(3) 若小明在点 $ A $ 朝着影子的方向以 $ v_1 $ 的速度匀速行走(图②),试求他影子的顶端在地面上移动的平均速度 $ v_2 $.

(1) 若小明距灯柱 $ OP $ 的水平距离 $ OA = a $,则他的影长 $ AC = $
$\frac{ah}{l - h}$
.(2) 若小明在两路灯之间行走,则他前后的两个影子的长度之和($ AC + AD $)是否不断改变? 为什么?
(3) 若小明在点 $ A $ 朝着影子的方向以 $ v_1 $ 的速度匀速行走(图②),试求他影子的顶端在地面上移动的平均速度 $ v_2 $.

答案:$\frac {ah}{l-h}$
解:(2)AC+AD为定值,理由如下:
由题意得AB//OP//O'P'
∵AB//OP
∴△ABC∽△OPC
∴$\frac {AB}{OP}=\frac {AC}{OC}$
∵AB=h,OP=O'P'=l,OA=a
∴$\frac h{l}=\frac {AC}{a+AC}$
∴$AC=\frac {ah}{l-h}$
同理可得$AD=\frac {(m-a)h}{l-h}$
∴$AC+AD=\frac {mh}{l-h}$
∴AC+AD为定值
(3)设点A到点O的距离为$S_{1},$点A到影子顶端C的距离为$S_{2}$
∵AB//OP
∴△ABC∽△OPC
∴$\frac {AB}{OP}=\frac {AC}{OC}$
∵AB=h,OP=l,$AC=S_{2},$$OC=OA+AC=S_{1}+S_{2}$
∴$\frac h{l}=\frac {S_{2}}{S_{1}+S_{2}}$
∴$\frac l{h}-1=\frac {S_{1}}{S_{2}}$
∴$\frac {S_{1}}{S_{2}}=\frac {v_{1}}{v_{2}}=\frac {l-h}h$
∴$v_{2}=\frac {hv_{1}}{l-h}$
解:(2)AC+AD为定值,理由如下:
由题意得AB//OP//O'P'
∵AB//OP
∴△ABC∽△OPC
∴$\frac {AB}{OP}=\frac {AC}{OC}$
∵AB=h,OP=O'P'=l,OA=a
∴$\frac h{l}=\frac {AC}{a+AC}$
∴$AC=\frac {ah}{l-h}$
同理可得$AD=\frac {(m-a)h}{l-h}$
∴$AC+AD=\frac {mh}{l-h}$
∴AC+AD为定值
(3)设点A到点O的距离为$S_{1},$点A到影子顶端C的距离为$S_{2}$
∵AB//OP
∴△ABC∽△OPC
∴$\frac {AB}{OP}=\frac {AC}{OC}$
∵AB=h,OP=l,$AC=S_{2},$$OC=OA+AC=S_{1}+S_{2}$
∴$\frac h{l}=\frac {S_{2}}{S_{1}+S_{2}}$
∴$\frac l{h}-1=\frac {S_{1}}{S_{2}}$
∴$\frac {S_{1}}{S_{2}}=\frac {v_{1}}{v_{2}}=\frac {l-h}h$
∴$v_{2}=\frac {hv_{1}}{l-h}$