9. 如图,在 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ AC = 2\sqrt{3} $,边 $ BC $ 上的中线 $ AD = 4 $.
(1) 求 $ \sin \angle DAC $、$ \tan B $ 的值;
(2) 求 $ \sin \angle BAD $ 的值.

(1) 求 $ \sin \angle DAC $、$ \tan B $ 的值;
(2) 求 $ \sin \angle BAD $ 的值.

答案:
解:(2)过点B作AD的垂线,交AD的延长线于点E
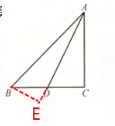
∵$sin∠DAC=\frac 12$
∴∠DAC=30°
∴∠BDE=∠ADC=60°
在Rt△BDE中,
∵BD=CD=2,∠BDE=60°
∴$BE=BD · sin 60°=\sqrt 3,$
DE=BD · cos 60°=1
在Rt△ABE中,
∵$BE=\sqrt 3,$AE=AD+DE=5
∴$AB=\sqrt {BE^2+AE^2}=2\sqrt 7$
∴$sin∠BAD=\frac {BE}{AB}=\frac {\sqrt {21}}{14}$
解:(2)过点B作AD的垂线,交AD的延长线于点E

∵$sin∠DAC=\frac 12$
∴∠DAC=30°
∴∠BDE=∠ADC=60°
在Rt△BDE中,
∵BD=CD=2,∠BDE=60°
∴$BE=BD · sin 60°=\sqrt 3,$
DE=BD · cos 60°=1
在Rt△ABE中,
∵$BE=\sqrt 3,$AE=AD+DE=5
∴$AB=\sqrt {BE^2+AE^2}=2\sqrt 7$
∴$sin∠BAD=\frac {BE}{AB}=\frac {\sqrt {21}}{14}$
10. 在 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $. 若 $ b = 2a $,则 $ \tan A = $
$\frac{1}{2}$
.答案:$\frac {1}{2}$
11. 在 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,若 $ AB = 2\sqrt{3} $,$ AC = 3 $,则 $ \angle A = $
$30°$
,$ \tan B = $$\sqrt{3}$
.答案:30°
$\sqrt{3}$
$\sqrt{3}$
12. 已知 $ \alpha $、$ \beta $ 为锐角. 若 $ \tan \alpha = \frac{\sqrt{3}}{3} $,$ \tan \beta = \sqrt{3} $,则 $ \beta - \alpha = $
$30°$
.答案:30°
13. 在 $ \triangle ABC $ 中,斜边 $ AB $ 是直角边 $ BC $ 的 4 倍,则 $ \cos A $ 等于(
A.$ \frac{1}{4} $
B.$ \frac{\sqrt{15}}{4} $
C.$ \frac{4\sqrt{15}}{15} $
D.$ 2\sqrt{2} $
B
).A.$ \frac{1}{4} $
B.$ \frac{\sqrt{15}}{4} $
C.$ \frac{4\sqrt{15}}{15} $
D.$ 2\sqrt{2} $
答案:B
14. 如图,已知 $ \odot O $ 的半径为 $ 5 \mathrm{ cm} $,弦 $ AB = 8 \mathrm{ cm} $,$ P $ 是 $ AB $ 延长线上的一点,$ BP = 2 \mathrm{ cm} $,则 $ \tan \angle OPA $ 等于(

A.$ \frac{3}{2} $
B.$ \frac{2}{3} $
C.$ 2 $
D.$ \frac{1}{2} $
D
).
A.$ \frac{3}{2} $
B.$ \frac{2}{3} $
C.$ 2 $
D.$ \frac{1}{2} $
答案:D
15. 如图,$ \triangle ABC $ 的顶点都是正方形网格中的格点,则 $ \sin \angle ABC $ 等于(

A.$ \sqrt{5} $
B.$ \frac{2\sqrt{5}}{5} $
C.$ \frac{\sqrt{5}}{5} $
D.$ \frac{2}{3} $
C
).
A.$ \sqrt{5} $
B.$ \frac{2\sqrt{5}}{5} $
C.$ \frac{\sqrt{5}}{5} $
D.$ \frac{2}{3} $
答案:C
16. 已知等腰三角形的周长为 16,一边长为 6. 求底角的余弦值.
答案:
解:①若腰长AB=AC=6,则BC=16-6×2=4
过点A作AD⊥BC,垂足为点D
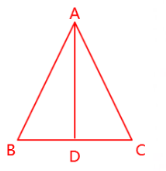
∵AB=AC=6,BC=4,AD⊥BC
∴点D为BC的中点
∴$BD=\frac 12BC=2$
∴$cosB=\frac {BD}{AB}=\frac 13$
②如果底边长BC=6,则腰长$AB=AC=\frac {16-6}2=5$
同理,$BD=\frac 12BC=3$
∴$cosB=\frac {BD}{AB}=\frac 35$
∴底角的余弦值为$\frac 13$或$\frac 35$
解:①若腰长AB=AC=6,则BC=16-6×2=4
过点A作AD⊥BC,垂足为点D

∵AB=AC=6,BC=4,AD⊥BC
∴点D为BC的中点
∴$BD=\frac 12BC=2$
∴$cosB=\frac {BD}{AB}=\frac 13$
②如果底边长BC=6,则腰长$AB=AC=\frac {16-6}2=5$
同理,$BD=\frac 12BC=3$
∴$cosB=\frac {BD}{AB}=\frac 35$
∴底角的余弦值为$\frac 13$或$\frac 35$