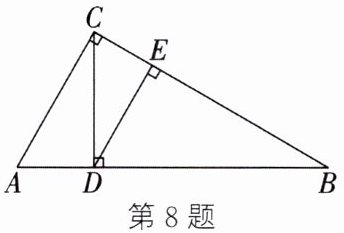
8. 如图,AC⊥BC 于点 C,CD⊥AB 于点 D,DE⊥BC 于点 E,其长度能表示点到直线(或线段)的距离的线段共有(
A.3条
B.4条
C.7条
D.8条
D
)
A.3条
B.4条
C.7条
D.8条
答案:8.D
解析:
表示点到直线距离的线段如下:
点$A$到$BC$的距离:$AC$;
点$B$到$AC$的距离:$BC$;
点$C$到$AB$的距离:$CD$;
点$A$到$CD$的距离:$AD$;
点$B$到$CD$的距离:$BD$;
点$D$到$BC$的距离:$DE$;
点$E$到$CD$的距离:$DE$(与上重复,应为点$B$到$DE$的距离:$BE$);
点$C$到$DE$的距离:$CE$。
共8条。
D
点$A$到$BC$的距离:$AC$;
点$B$到$AC$的距离:$BC$;
点$C$到$AB$的距离:$CD$;
点$A$到$CD$的距离:$AD$;
点$B$到$CD$的距离:$BD$;
点$D$到$BC$的距离:$DE$;
点$E$到$CD$的距离:$DE$(与上重复,应为点$B$到$DE$的距离:$BE$);
点$C$到$DE$的距离:$CE$。
共8条。
D
9. (易错题)在直线 AB 上任取一点 O,过点 O 作射线 OC,OD,使 OC⊥OD. 当∠AOC=30°时,∠BOD 的度数为
60°或120°
.答案:9.60°或120° [易错分析]未给出图形,考虑不周全致错.
解析:
当OC、OD在直线AB同侧时:
∵OC⊥OD,∠AOC=30°
∴∠AOD=∠COD - ∠AOC=90° - 30°=60°
∵∠AOD + ∠BOD=180°
∴∠BOD=180° - 60°=120°
当OC、OD在直线AB异侧时:
∵OC⊥OD,∠AOC=30°
∴∠BOD=180° - ∠AOC - ∠COD=180° - 30° - 90°=60°
综上,∠BOD的度数为60°或120°
∵OC⊥OD,∠AOC=30°
∴∠AOD=∠COD - ∠AOC=90° - 30°=60°
∵∠AOD + ∠BOD=180°
∴∠BOD=180° - 60°=120°
当OC、OD在直线AB异侧时:
∵OC⊥OD,∠AOC=30°
∴∠BOD=180° - ∠AOC - ∠COD=180° - 30° - 90°=60°
综上,∠BOD的度数为60°或120°
10. (2025·启东期中)如图,直线 AB 和 CD 相交于点 O,CO⊥OE,OF 平分∠AOE,∠COF=34°,则∠BOE 的度数为
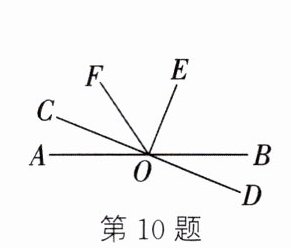
68°
.
答案:10.68°
解析:
解:
∵CO⊥OE,
∴∠COE=90°,
∵∠COF=34°,
∴∠EOF=∠COE - ∠COF=90° - 34°=56°,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=2×56°=112°,
∵∠AOB=180°,
∴∠BOE=∠AOB - ∠AOE=180° - 112°=68°.
故∠BOE的度数为68°.
∵CO⊥OE,
∴∠COE=90°,
∵∠COF=34°,
∴∠EOF=∠COE - ∠COF=90° - 34°=56°,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=2×56°=112°,
∵∠AOB=180°,
∴∠BOE=∠AOB - ∠AOE=180° - 112°=68°.
故∠BOE的度数为68°.
11. 如图,AC⊥BC 于点 C,AD⊥CD 于点 D,AB=5,AD=3,则 AC 长的取值范围是
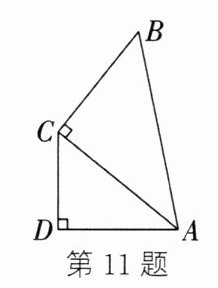
3<AC<5
.
答案:11.3<AC<5
解析:
解:在 $Rt\triangle ADC$ 中,$AD ⊥ CD$,$AD = 3$,根据直角三角形斜边大于直角边,得 $AC > AD = 3$;
在 $Rt\triangle ACB$ 中,$AC ⊥ BC$,$AB = 5$,同理可得 $AC < AB = 5$。
综上,$AC$ 长的取值范围是 $3 < AC < 5$。
$3 < AC < 5$
在 $Rt\triangle ACB$ 中,$AC ⊥ BC$,$AB = 5$,同理可得 $AC < AB = 5$。
综上,$AC$ 长的取值范围是 $3 < AC < 5$。
$3 < AC < 5$
12. 如图,∠ACB=90°,BC=6,AC=8,AB=10,点 D 在线段 AB 上运动,则线段 CD 长的最小值是
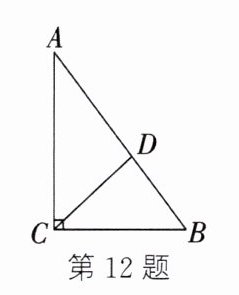
4.8
.
答案:12.4.8
解析:
解:当$CD ⊥ AB$时,$CD$最短。
$\because \angle ACB = 90°$,
$\therefore S_{\triangle ABC} = \frac{1}{2}AC · BC = \frac{1}{2}AB · CD$。
$\because AC = 8$,$BC = 6$,$AB = 10$,
$\therefore \frac{1}{2} × 8 × 6 = \frac{1}{2} × 10 × CD$,
解得$CD = \frac{48}{10} = 4.8$。
故线段$CD$长的最小值是$4.8$。
$\because \angle ACB = 90°$,
$\therefore S_{\triangle ABC} = \frac{1}{2}AC · BC = \frac{1}{2}AB · CD$。
$\because AC = 8$,$BC = 6$,$AB = 10$,
$\therefore \frac{1}{2} × 8 × 6 = \frac{1}{2} × 10 × CD$,
解得$CD = \frac{48}{10} = 4.8$。
故线段$CD$长的最小值是$4.8$。
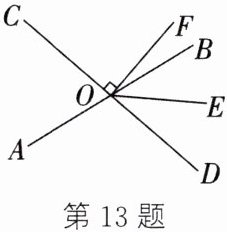
13. 如图,直线 AB,CD 相交于点 O,OE 平分∠BOD,OF⊥CD.
(1)若∠EOF=54°,求∠AOC 的度数.
(2)① 在∠AOD 的内部作射线 OG⊥OE;
② 试探索∠AOG 与∠EOF 之间有怎样的数量关系,并说明理由.
(1)若∠EOF=54°,求∠AOC 的度数.
(2)① 在∠AOD 的内部作射线 OG⊥OE;
② 试探索∠AOG 与∠EOF 之间有怎样的数量关系,并说明理由.

答案:
13.(1)因为OF⊥CD,所以∠DOF = 90°.因为∠EOF = 54°,所以∠DOE = 90° - 54° = 36°.又因为OE平分∠BOD,所以∠BOD = 2∠DOE = 72°.所以∠AOC = ∠BOD = 72°
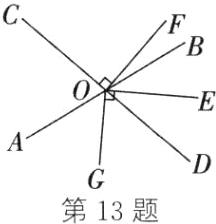
(2)①如图所示 ②∠AOG = ∠EOF 理由:因为OE平分∠BOD,所以∠BOE = ∠DOE.因为OF⊥CD,OG⊥OE,所以∠EOF + ∠DOE = 90°,∠AOG + ∠BOE = 90°.所以∠AOG = ∠EOF.
13.(1)因为OF⊥CD,所以∠DOF = 90°.因为∠EOF = 54°,所以∠DOE = 90° - 54° = 36°.又因为OE平分∠BOD,所以∠BOD = 2∠DOE = 72°.所以∠AOC = ∠BOD = 72°
(2)①如图所示 ②∠AOG = ∠EOF 理由:因为OE平分∠BOD,所以∠BOE = ∠DOE.因为OF⊥CD,OG⊥OE,所以∠EOF + ∠DOE = 90°,∠AOG + ∠BOE = 90°.所以∠AOG = ∠EOF.

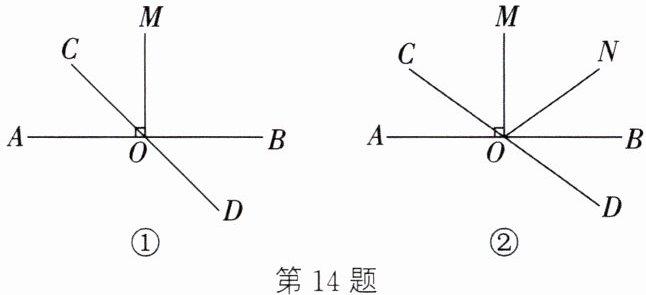
14. 已知直线 AB 与 CD 相交于点 O,OM⊥AB.
(1)如图①,若 OC 平分∠AOM,求∠AOD 的度数;
(2)如图②,若∠BOC=4∠NOB,且 OM 平分∠NOC,求∠MON 的度数.
(1)如图①,若 OC 平分∠AOM,求∠AOD 的度数;
(2)如图②,若∠BOC=4∠NOB,且 OM 平分∠NOC,求∠MON 的度数.

答案:14.(1)因为OM⊥AB,所以∠AOM = 90°.因为OC平分∠AOM,所以∠AOC = $\frac{1}{2}$∠AOM = 45°.因为∠AOC + ∠AOD = 180°,所以∠AOD = 180° - ∠AOC = 180° - 45° = 135°
(2)因为∠BOC = 4∠NOB,所以设∠NOB = x,则∠BOC = 4x.所以∠NOC = ∠BOC - ∠NOB = 3x.因为OM平分∠NOC,所以∠COM = ∠MON = $\frac{1}{2}$∠NOC = $\frac{3}{2}$x.因为OM⊥AB,所以∠BOM = 90°.因为∠BOM = ∠MON + ∠NOB,所以$\frac{3}{2}$x + x = 90°.所以x = 36°.所以∠MON = $\frac{3}{2}$x = 54°,即∠MON的度数为54°
(2)因为∠BOC = 4∠NOB,所以设∠NOB = x,则∠BOC = 4x.所以∠NOC = ∠BOC - ∠NOB = 3x.因为OM平分∠NOC,所以∠COM = ∠MON = $\frac{1}{2}$∠NOC = $\frac{3}{2}$x.因为OM⊥AB,所以∠BOM = 90°.因为∠BOM = ∠MON + ∠NOB,所以$\frac{3}{2}$x + x = 90°.所以x = 36°.所以∠MON = $\frac{3}{2}$x = 54°,即∠MON的度数为54°