12. (2025·温州期末)骑行电瓶车时戴安全帽可以大幅度减少因交通事故引发的人身伤害,为此交警部门在我市广泛开展了此项宣传活动。在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,将收集的数据制成统计表和如图所示的统计图。
活动前骑电瓶车戴安全帽情况统计表
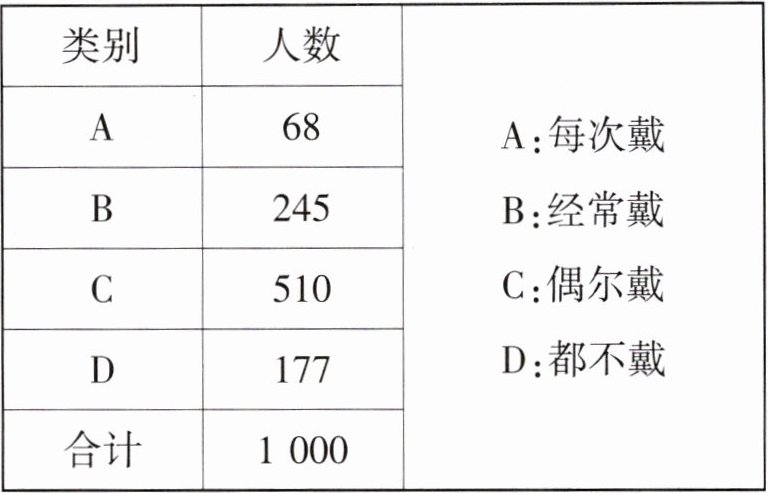
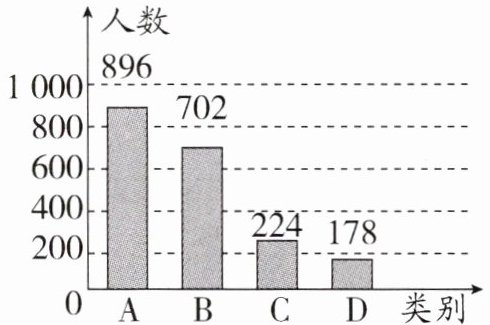
(1)宣传活动前,在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?
(2)宣传活动后,抽取的样本容量是
(3)该市约有30万人使用电瓶车,请估计活动前全市骑电瓶车“经常戴”安全帽的总人数。
(4)小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178,反而比活动前增加了1人,因此交警部门开展的宣传活动没有效果。小明分析数据的方法是否合理?请结合统计图表,对数据分析,并谈谈你对交警部门宣传活动的效果的看法。
活动前骑电瓶车戴安全帽情况统计表


(1)宣传活动前,在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?
(2)宣传活动后,抽取的样本容量是
2000
。(3)该市约有30万人使用电瓶车,请估计活动前全市骑电瓶车“经常戴”安全帽的总人数。
(4)小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178,反而比活动前增加了1人,因此交警部门开展的宣传活动没有效果。小明分析数据的方法是否合理?请结合统计图表,对数据分析,并谈谈你对交警部门宣传活动的效果的看法。
答案:12.(1)$\because 510 > 245 > 177 > 68$,$\therefore$宣传活动前,在抽取的市民中“偶尔戴”的人数最多,占抽取人数的$\frac{510}{1000}× 100\% = 51\%$。
(2)2000解析:依题意得样本容量$= 896 + 702 + 224 + 178 = 2000$。
(3)估计活动前全市骑电瓶车“经常戴”安全帽的总人数为$30× \frac{245}{1000} = 7.35$(万人)。
(4)小明分析数据的方法不合理。宣传活动后骑电瓶车“都不戴”安全帽所占的百分比为$\frac{178}{896 + 702 + 224 + 178}× 100\% = 8.9\%$,宣传活动前骑电瓶车“都不戴”安全帽所占的百分比为$\frac{177}{1000}× 100\% = 17.7\%$。$\because 8.9\% < 17.7\%$,$\therefore$交警部门开展的宣传活动有效果。
(2)2000解析:依题意得样本容量$= 896 + 702 + 224 + 178 = 2000$。
(3)估计活动前全市骑电瓶车“经常戴”安全帽的总人数为$30× \frac{245}{1000} = 7.35$(万人)。
(4)小明分析数据的方法不合理。宣传活动后骑电瓶车“都不戴”安全帽所占的百分比为$\frac{178}{896 + 702 + 224 + 178}× 100\% = 8.9\%$,宣传活动前骑电瓶车“都不戴”安全帽所占的百分比为$\frac{177}{1000}× 100\% = 17.7\%$。$\because 8.9\% < 17.7\%$,$\therefore$交警部门开展的宣传活动有效果。