1. 一个圆锥的底面半径是 4 分米,高是 6 分米,它的底面积是(
50.24
)平方分米,体积是(100.48
)立方分米。答案:1. 50.24 100.48
解析:
底面积:$S = \pi r^2 = 3.14×4^2 = 3.14×16 = 50.24$(平方分米)
体积:$V = \frac{1}{3}Sh = \frac{1}{3}×50.24×6 = 50.24×2 = 100.48$(立方分米)
50.24 100.48
体积:$V = \frac{1}{3}Sh = \frac{1}{3}×50.24×6 = 50.24×2 = 100.48$(立方分米)
50.24 100.48
2. (2025·泰州姜堰区期末)小华把一个底面积是 18 平方厘米、高是 6 厘米的圆锥形橡皮泥捏成一个圆柱,这个圆柱可以是底面积(
6
)平方厘米、高 6 厘米,也可以是底面积 18 平方厘米、高(2
)厘米。答案:2. 6 2
3. 一个圆柱和一个圆锥等底等高,体积相差 18 立方厘米。圆柱的体积是(
27
)立方厘米,圆锥的体积是(9
)立方厘米。答案:3. 27 9
解析:
因为圆柱和圆锥等底等高,所以圆柱体积是圆锥体积的3倍。设圆锥体积为$V$,则圆柱体积为$3V$。体积相差$3V - V = 2V = 18$立方厘米,解得$V = 9$立方厘米,圆柱体积为$3V = 27$立方厘米。
27;9
27;9
4. 亮点原创·右图圆柱形容器内的水占圆柱形容器容积的$\frac{1}{3}$,倒入圆锥形容器(

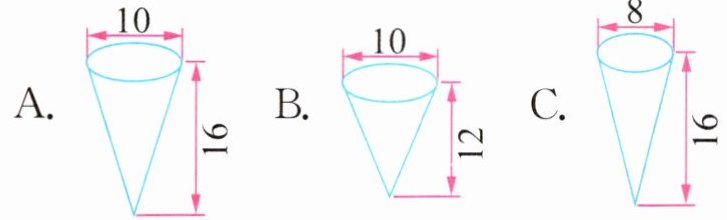
C.
A
)内正好倒满。(单位:cm)

C.
答案:4. A
5. (南京溧水区期末)如图,健身房有一个圆柱形沙包,量得沙包的底面直径是 2 分米,高是 8 分米,在一次训练中,沙包底破了,沙子全部流到了地上形成了一个高 4 分米的圆锥形沙堆,这个沙堆的占地面积是多少平方分米?


答案:$5. 3.14×(2÷2)^2×8=25.12($立方分米)
25.12×3÷4=18.84(平方分米)
25.12×3÷4=18.84(平方分米)
6. 把一个棱长为 6 分米的正方体木料削成一个最大的圆锥,需要削去(
159.48
)立方分米的木料。答案:6. 159.48 解析 把正方体削成一个最大的圆锥,这个圆锥的底面直径和高都等于正方体的棱长6分米,那么削去部分的体积就是$6×6×6−3.14×(6÷2)^2×6×\frac{1}{3}=159.48($立方分米)。
解析:
$6×6×6 - 3.14×(6÷2)^2×6×\frac{1}{3}$
$=216 - 3.14×9×6×\frac{1}{3}$
$=216 - 3.14×18$
$=216 - 56.52$
$=159.48$(立方分米)
$=216 - 3.14×9×6×\frac{1}{3}$
$=216 - 3.14×18$
$=216 - 56.52$
$=159.48$(立方分米)
7. 鞍山玉佛山书画院是鞍山唯一的一座水上书画院,其设计可以近似看成一个圆柱和圆锥的组合体。奇奇用橡皮泥制作了一个模型(如图),已知圆锥部分与圆柱部分高之比为$9:7$,该模型的总体积为$274.75\ \mathrm{cm}^3$,模型中圆锥部分的高是多少?
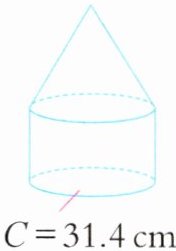

答案:7. 圆锥部分与圆柱部分体积之比为(9÷3):7=
$3:7 274.75×\frac{3}{3+7}=82.425(cm^3) 31.4$
÷3.14÷2=5(cm) 82.425×3÷(3.14×
$5^2)=3.15(cm)$
$3:7 274.75×\frac{3}{3+7}=82.425(cm^3) 31.4$
÷3.14÷2=5(cm) 82.425×3÷(3.14×
$5^2)=3.15(cm)$
8. 如图,瓶底的面积与杯口的面积相等,将瓶中的液体倒入杯子中,能倒满(

6
)杯。
答案:8. 6 解析 令瓶底与杯口的面积为S,则瓶中液体的体积为2Sh,杯子的体积为$\frac{1}{3}Sh,$所以能倒满$2Sh÷\frac{1}{3}Sh=6($杯)。
9. 如图,一个圆锥形容器中装有 3 升水,水面高度正好是圆锥形容器高度的$\frac{1}{2}$,这个容器的容积是多少升?(忽略容器壁厚度)


答案:$9. \frac{1}{2}r:r=1:2 \frac{1}{2}h:h=1:2$
V_小:V_大$=(1^2×1×\frac{1}{3}):(2^2×2×\frac{1}{3})=1:8$
3×8=24(升) 解析 根据水面的高度与容器的高度的比为1:2,水面半径和容器底面半径的比为1:2,可得水的体积与容器的容积的比为$(1^2×1×\frac{1}{3}):(2^2×2×\frac{1}{3})=1:8,$这个容器的容积就是3×8=24(升)。
V_小:V_大$=(1^2×1×\frac{1}{3}):(2^2×2×\frac{1}{3})=1:8$
3×8=24(升) 解析 根据水面的高度与容器的高度的比为1:2,水面半径和容器底面半径的比为1:2,可得水的体积与容器的容积的比为$(1^2×1×\frac{1}{3}):(2^2×2×\frac{1}{3})=1:8,$这个容器的容积就是3×8=24(升)。